Revista Boliviana de Química
versión On-line ISSN 0250-5460
Rev. Bol. Quim vol.33 no.2 La Paz jul. 2016
ARTICULOS ORIGINALES
Acoustic properties and volumetric data of liquid mixtures containing valeronitrile and esteres; effects due to temperature changes
Propiedades acústicas y datos volumétricos de mezclas líquidas que contienen valeronitrilo y esteres; efectos debidos a los cambios de temperatura.
Salvador H. Canzonieri1, Alejandra B. Mariano1,2,*, Alberto G. Camacho1, Diego G. Salgado3, Luis Romaní3
1 Facultad de Ingeniería, Universidad Nacional del Comahue, Buenos Aires 1400, +542994490340, Neuquén (8300), Argentina, salvador.canzonieri@fain.uncoma.edu.ar, alejandra.mariano@fain.uncoma.edu.ar, alberto.camacho@fain.uncoma.edu.ar
2Consejo Nacional de Investigaciones Científicas y Técnicas (CONICET), Neuquén (8300), Argentina, alejandra.mariano@fain.uncoma.edu.ar
3Facultad de Ciencias del Campus de Ourense, Universidad de Vigo, E 32004 Ourense, Vigo, España.
*Corresponding author: alejandra.mariano@fain.uncoma.edu.ar
Abstract
In this work experimental data of density, ρ, and velocity of sound, u, of the binary systems of valeronitrile and methyl propanoate, and valeronitrile and ethyl propanoate, at atmospheric pressure and in a range of temperature from 278.15 K to 318.15 K were reported. From experimental information, molar volume, V(x, T), excess molar volume, VE(x, T), thermal expansion coefficient, ![]() (x, T), thermal expansion coefficient of excess,
(x, T), thermal expansion coefficient of excess, ![]() E(x,T), velocity of sound deviation, Δu(x, T), isentropic compressibility, ks(x,T) and isentropic compressibility of excess, ksE(x, T), were calculated. Each set of excess results was fitted to a polynomial equation like Redlich and Kister [1] as a function of composition and temperature, with deviations within the range of experimental error. Binary mixtures studied showed negative values of
E(x,T), velocity of sound deviation, Δu(x, T), isentropic compressibility, ks(x,T) and isentropic compressibility of excess, ksE(x, T), were calculated. Each set of excess results was fitted to a polynomial equation like Redlich and Kister [1] as a function of composition and temperature, with deviations within the range of experimental error. Binary mixtures studied showed negative values of ![]() E, Δu y ksE, over the whole composition and temperature range. Also, velocity of sound was predicted with the models proposed by Nomoto [2,3], Van Dael [4] and Ernst et al. [5].
E, Δu y ksE, over the whole composition and temperature range. Also, velocity of sound was predicted with the models proposed by Nomoto [2,3], Van Dael [4] and Ernst et al. [5].
Keywords: Excess molar volume, Thermal expansion coefficient, Isentropic compressibility, Valeronitrile, Methyl propanoate, Ethyl propanoate
Resumen
En este trabajo se reportan los datos experimentales de densidad, ρ, y de la velocidad del sonido u, de sistemas binarios de valeronitrilo y propanoato de metilo, y de valeronitrilo y propanotao de etilo, a presión atmosférica y en un rango de temperatura entre 278,15 K y 318,15 K . El volumen molar, V(x, T), el volumen molar de exceso, VE(x, T), el coeficiente de expansión térmica, ![]() (x, T), el coeficiente de exceso de expansión térmica,
(x, T), el coeficiente de exceso de expansión térmica, ![]() E(x, T), la desviación de la velocidad del sonido, uΔ(x, T), la compresibilidad isentrópica, ks(x, T) y la compresibilidad isentrópica de exceso, ksE(x, T), fueron calculados. Cada conjunto de resultados de exceso se ajustó a una ecuación polinómica como Redlich y Kister [1] como una función de la composición y de la temperatura, con desviaciones dentro de la gama de error experimental. Las mezclas binarias estudiadas mostraron valores negativos de
E(x, T), la desviación de la velocidad del sonido, uΔ(x, T), la compresibilidad isentrópica, ks(x, T) y la compresibilidad isentrópica de exceso, ksE(x, T), fueron calculados. Cada conjunto de resultados de exceso se ajustó a una ecuación polinómica como Redlich y Kister [1] como una función de la composición y de la temperatura, con desviaciones dentro de la gama de error experimental. Las mezclas binarias estudiadas mostraron valores negativos de ![]() E, uΔ y ksE, sobre todo el rango de composición y temperatura. Adicionalmente, se predijo la velocidad del sonido con los modelos propuestos por Nomoto [2,3], Van Dael [4] y Ernst et al. [5].
E, uΔ y ksE, sobre todo el rango de composición y temperatura. Adicionalmente, se predijo la velocidad del sonido con los modelos propuestos por Nomoto [2,3], Van Dael [4] y Ernst et al. [5].
INTRODUCCION
El estudio de las propiedades volumétricas de mezclas binarias y ternarias en fase líquida proporciona información sobre la estructura de los componentes individuales en la mezcla, las cuales son necesarias en el diseño de procesos industriales. El cálculo experimental de los volúmenes de exceso constituye una interesante fuente de información para el estudio de las diferencias que se producen en estas mezclas con respecto al comportamiento ideal y permite valorar la capacidad predictiva de los modelos moleculares de disoluciones.
En forma similar, las propiedades acústicas, por ejemplo, las velocidades del sonido y las compresibilidades isentrópicas y compresibilidades isentrópicas de exceso derivadas de ellas, son muy útiles para comprobar el tipo y la naturaleza de las interacciones presentes a nivel molecular en los componentes de la mezcla.
Nuestro grupo de investigación viene trabajando desde hace varios años sobre mezclas líquidas que contienen moléculas no polares y polares [6-10]. Dentro de esta línea trabajamos en forma experimental y teórica con sistemas binarios y ternarios de esteres alifáticos, hidrocarburos aromáticos y nitrilos lineales. Además del interés científico que se refleja en este tipo de mezclas, son también de importancia a nivel industrial ya que se encuentran presentes en un gran número de procesos.
Los esteres alifáticos son productos químicos importantes para la industria, y sus mezclas binarias con moléculas polares y no polares, han recibido amplia atención, especialmente para entender el comportamiento del oxígeno carbonilo en el grupo éster, -COO- y los grupos metilenos -CH2- de las cadenas alifáticas laterales de R o R' en R-COOR', dentro de la mezcla. [11,12].
En particular, como una continuación del estudio que realizamos y como parte de nuestro programa de investigación en curso, en este trabajo se presentan datos de densidad y velocidad del sonido de las mezclas binarias valeronitrilo + propanoato de metilo y valeronitrilo + propanoato de etilo, en todo el rango de composición, a las temperaturas de 278,15; 283,15; 288,15; 293,15; 298,15; 303,15; 308,15; 313,15 y 318,15 K y a presión atmosférica. El aporte de estos nuevos datos experimentales permite también su utilización en la comprobación, perfeccionamiento y obtención de parámetros de modelos semiempíricos y teóricos, los cuales tienen una importante aplicación en el diseño y construcción de equipos industriales.
EXPERIMENTAL
Metodología Productos utilizados
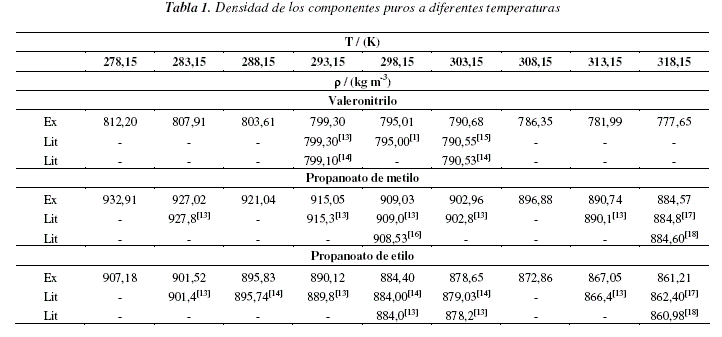
Los productos químicos utilizados en este trabajo de investigación fueron valeronitrilo (> 99,5 %), propanoato de etilo (> 99,0 %) y propanoato de metilo (> 99,0 %), los dos primeros suministrados por Aldrich y el tercer producto por Fluka, todos los compuestos fueron tratados previamente a su utilización. Fueron deshumidificados con tamices moleculares Fluka 4 Å, producto desecante para reducir al mínimo la presencia de humedad, y se desgasificaron mediante un equipo de ultrasonido. En las tablas 1 y 2 se comparan los valores experimentales de densidad y velocidad del sonido a las distintas temperaturas con los datos disponibles en la literatura; en general, el grado de concordancia obtenido es bueno.
Dispositivos experimentales
El equipo utilizado para realizar las determinaciones experimentales ha sido el Anton-Paar DSA 48, que realiza dos funciones simultáneamente, medir la densidad y la velocidad del sonido para la misma muestra. Para ello posee dos células de medida conectadas en serie, una para cada propiedad a medir.
En lo que respecta a la densidad, la célula de medida esta formada por un tubo de vidrio (Duran 20) con forma de U, recubierto por una camisa también de vidrio, todo el conjunto está rodeado por un recinto termostático de cobre que controla la temperatura de la célula por efecto Peltier. La célula de medida de la velocidad del sonido se encuentra situada encima de la célula de medida de la densidad, y ubicada en una cavidad hecha de teflón que está rodeada lateralmente por el transmisor-receptor de pulsos ultrasónicos, cuya superficie es de acero inoxidable.
La transmisión de calor entre el termostato de cobre y el tubo en U se ve favorecida por la presencia de un gas de alta conductividad térmica en el espacio que hay entre la camisa y el tubo, que facilita el equilibrio térmico entre la muestra y el sistema de termostatización. La medida de la temperatura de todo el sistema se realiza mediante un termistor situado en la célula de densidad con una precisión de ±0,01 K. El error en la estimación de la densidad es menor a 0,01 kg m-3 y en la velocidad del sonido menor a 0,05 m s-1.
RESULTADOS Y DISCUSIÓN
En las tablas 3 y 4 se presentan los valores experimentales de densidad y velocidad del sonido de las mezclas binarias estudiadas a distintas temperaturas. A partir de los datos experimentales se calcularon el volumen molar de exceso, VE, el coeficiente de expansión térmica, ![]() D, el coeficiente de expansión térmica de exceso,
D, el coeficiente de expansión térmica de exceso, ![]() E, la desviación de la velocidad del sonido, Δu, la compresibilidad isoentrópica, ks, y la compresibilidad isoentrópica de exceso, ksE, utilizando las expresiones detalladas a continuación.
E, la desviación de la velocidad del sonido, Δu, la compresibilidad isoentrópica, ks, y la compresibilidad isoentrópica de exceso, ksE, utilizando las expresiones detalladas a continuación.
El volumen molar de exceso de una mezcla particular se puede calcular con la expresión dada a continuación. Donde xi es la fracción molar del componente i en la mezcla, Mi es la masa molar del componente, ρ es la densidad de la mezcla, ρ¡ la densidad del componente i, y n es el número de componentes de la mezcla. El error estimado para VE es ±2 10-9 m3 mol-1.
![]()
El coeficiente de expansión térmica a se puede obtener a partir de la ecuación de ajuste de las densidades ρ = ρ(T), por derivación analítica de dicha ecuación respecto de la temperatura. La incertidumbre estimada para ![]() es ±0,003 kK-1.
es ±0,003 kK-1.

El coeficiente de expansión térmica isobárico de exceso, ![]() E, es posible calcularlo a partir de los volúmenes de exceso a diferentes temperaturas usando la ecuación termodinámica que sigue.
E, es posible calcularlo a partir de los volúmenes de exceso a diferentes temperaturas usando la ecuación termodinámica que sigue.

La reproducibilidad en la medición de la densidad produce una propagación del error para el volumen molar de exceso, de aproximadamente 2.10-9 m3mol-1. La incertidumbre de ![]() E, dependiente de lo anterior, se estima en el orden de 10-6 K-1, valor también indicado en la bibliografía [21,22].
E, dependiente de lo anterior, se estima en el orden de 10-6 K-1, valor también indicado en la bibliografía [21,22].
A partir de los datos de velocidad del sonido, se puede calcular la desviación de la velocidad del sonido a partir de la siguiente ecuación:
![]()
Siendo u la velocidad del sonido de la mezcla y ui la velocidad del sonido del componente puro. El error en Δu se estima en ±0,1 ms-1.
La compresibilidad isoentrópica, ks, se obtiene a partir de las densidades y las velocidades del sonido haciendo uso de la ecuación de Laplace, que se presenta a continuación. La precisión en la determinación de la compresibilidad isoentrópica se estimó en ±0,05 TPa-1.
![]()
Se puede calcular la compresibilidad isoentrópica de exceso, ksE, a partir de la siguiente ecuación:
![]()
Donde la expresión para la compresibilidad isoentrópica de la mezcla ideal se deriva de la definición del coeficiente de compresibilidad isotérmica, kT, y extendida a la idealidad [21]. Acordando con [21], ksid se calcula como:
![]()
Donde: ![]()
Siendo C°p.1 y C°p.2 las capacidades caloríficas molares isobáricas de los componentes 1 y 2; x1 y x2 son las fracciones molares de los componentes 1 y 2; y Φ1 y Φ2 las fracciones en volumen de los componentes 1 y 2, definidas por:

Las densidades, velocidades del sonido, compresibilidades isoentrópicas, y coeficientes de expansión térmica se han ajustado para cada sistema a un polinomio del tipo:
![]()
Donde Y es la propiedad, x es la fracción molar, Aij son los coeficientes de ajuste, T es la temperatura y T0 es una temperatura de referencia.
Las magnitudes de exceso se han ajustado a la siguiente ecuación del tipo Redlich y Kister:
![]()
En todos los casos los valores de los coeficientes se han obtenido mediante el método de mínimos cuadrados con dos variables de ajuste, temperatura y composición. Donde YmE representa VE, ![]() E, Δu, o kse y x es la fracción molar del componente 1, Aij son los coeficientes de ajuste obtenidos por mínimos cuadrados.
E, Δu, o kse y x es la fracción molar del componente 1, Aij son los coeficientes de ajuste obtenidos por mínimos cuadrados.
Los coeficientes Aij se dan en las tablas 5 y 6, junto con la desviación estándar (σ) definida como:

Siendo n el número de datos experimentales y p el número de coeficientes de la ecuación.
La figura 1 muestra los valores experimentales obtenidos, para el sistema binario valeronitrilo + propanoato de metilo de VE, kse y ![]() E, junto con los valores obtenidos con la ecuación de ajuste de Redlich y Kister [1], en función de la fracción molar del componente 1.
E, junto con los valores obtenidos con la ecuación de ajuste de Redlich y Kister [1], en función de la fracción molar del componente 1.
En la figura 2 se representan, de forma similar, las mismas propiedades, correspondientes al otro sistema estudiado, valeronitrilo + propanoato de etilo.
Las figuras 1 y 2 muestran que la mezcla binaria valeronitrilo + propanoato de metilo muestra curvas positivas para el volumen molar de exceso, VE, en todo el rango de fracciones molares y temperaturas, estos valores son menos positivos a medida que se incrementa la temperatura. Esta propiedad presenta una curva sigmoidea para el sistema valeronitrilo + propanoato de etilo, con valores positivos para composiciones pequeñas de propanoato de etilo, con el incremento de la temperatura, el volumen molar de exceso toma valores mas negativos para casi todo el rango de fracciones molares, salvo para composiciones pequeñas del ester, donde con un aumento de temperatura se producen valores menos positivos.
La mezcla binaria valeronitrilo + propanoato de metilo, muestra, para la compresibilidad isoentrópica de exceso, kse, curvas positivas para las temperaturas mas bajas y negativas a partir de los 288,15 K, para todo el rango de concentraciones. Según puede verse en la figura 1, la propiedad estudiada presenta cambios apreciables frente a la variación de temperatura.
El sistema binario valeronitrilo + propanoato de etilo presenta valores negativos de la compresibilidad isoentrópica de exceso, kse, para todo el rango de concentración y para todas las temperaturas analizadas como se puede observar en la figura 2, en todos los casos éstos son más negativos al aumentar la temperatura, y se observa, al igual que para el otro sistema, que presentan una variación con la temperatura muy significativa. La kse muestra valores que varían en sentido contrario con el aumento de la temperatura para la mezcla valeronitrilo + propanoato de etilo.
Se realizó el cálculo de la velocidad del sonido para este sistema binario con los siguientes modelos predictivos: la relación empírica de Nomoto [2,3], la relación de mezcla ideal de Van Dael [4] y el modelo de velocidad media del sonido respecto al tiempo de un impulso de Ernst [5].
El objetivo de esta parte del trabajo es comparar los métodos más comunes de cálculo del "exceso", en el sentido de la desviaciones de los valores experimentales, respecto de los valores teóricos de la velocidad de sonido para las mezclas líquidas estudiadas, es decir, fueron examinadas las ventajas relativas de estas teorías y relaciones comparando los valores teóricos de velocidades ultrasónicas con aquellos obtenidos experimentalmente.
Se realizó el cálculo de la velocidad del sonido de la mezcla binaria, utilizando información experimental de los componentes puros, con los modelos predictivos mencionados:

Siendo x vol.1 la fracción en volumen del componente 1.
En las figuras 3 y 4 se muestra los valores experimentales y teóricos de la velocidad del sonido, u, de los sistemas a las distintas temperaturas de trabajo, para todo el rango de concentraciones.
Las velocidades ultrasónicas calculadas, junto con las velocidades experimentales, el porcentaje de error en las predicciones respecto de los valores experimentales y las desviaciones de los valores experimentales respecto de los teóricos, uEXP. - uCALC., para cada fracción molar, y a 298,15 K, de los dos sistemas estudiados, se muestran en la tabla 7.
En la figura 5 se graficó, para los dos sistemas estudiados: valeronitrilo + propanoato de metilo y valeronitrilo + propanoato de metilo, la diferencia de la velocidad del sonido entre los valores experimentales y los teóricos, uEXP. - uCALC., en función de la fracción molar del componente 1 y a 298,15 K.
La predicción de las velocidades del sonido del sistema produjo buenos resultados con los tres modelos aplicados, y para todas las temperaturas estudiadas, como se muestra en las figuras 3 y 4. Las predicciones obtenidas con los modelos de Nomoto y de Ernst concuerdan mejor con los valores experimentales de la velocidad que la relación de Van Dael para la mezcla valeronitrilo + propanoato de metilo. Mientras que para el sistema valeronitrilo + propanoato de etilo la predicción de Van Dael concuerda mejor con los valores experimentales, aunque los tres modelos muestran desviaciones muy pequeñas entre los datos experimentales y los teóricos para el caso de esta mezcla.
CONCLUSIONES
La mezcla binaria valeronitrilo + propanoato de metilo presentó valores positivos para el volumen molar de exceso, VE, en todo el rango de fracciones molares y temperaturas, siendo menos positivos a medida que se incrementa la temperatura. Para el sistema valeronitrilo + propanoato de etilo se obtuvieron valores de VE positivos para composiciones pequeñas de propanoato de etilo y valores negativos para el resto de las composiciones.
Los valores de la compresibilidad isoentrópica de exceso, ksE, resultaron, en general, negativos para ambos sistemas estudiados. La mezcla binaria valeronitrilo + propanoato de metilo presentó valores positivos a bajas temperaturas..
Las otras dos propiedades estudiadas: coeficiente de expansión térmica de exceso, ![]() E, y desviación de la velocidad del sonido, Au, presentaron valores negativos para los dos sistemas objeto de estudio.El comportamiento indicado es característico de los sistemas que no presentan fuertes interacciones específicas. Cuando el efecto predominante en el proceso de mezcla es la ruptura de estructuras y la expansión de las mismas, el desplazamiento del sonido mediante ondas longitudinales a través de la mezcla se verá perjudicado, se recorrerá el mismo espacio en mayor tiempo, dando velocidades del sonido menores, con lo que las desviaciones, Au, respecto al comportamiento ideal serán negativas.
E, y desviación de la velocidad del sonido, Au, presentaron valores negativos para los dos sistemas objeto de estudio.El comportamiento indicado es característico de los sistemas que no presentan fuertes interacciones específicas. Cuando el efecto predominante en el proceso de mezcla es la ruptura de estructuras y la expansión de las mismas, el desplazamiento del sonido mediante ondas longitudinales a través de la mezcla se verá perjudicado, se recorrerá el mismo espacio en mayor tiempo, dando velocidades del sonido menores, con lo que las desviaciones, Au, respecto al comportamiento ideal serán negativas.
La predicción de las velocidades del sonido del sistema produjo buenos resultados con los tres modelos aplicados, y para todas las temperaturas estudiadas,
RECONOCIMIENTOS
Se agradece el aporte, en la realización de este trabajo, de la Universidad Nacional del Comahue y CONICET, ambos de Argentina y de la Universidad de Vigo, Facultad de Ciencias del Campus de Ourense, España.
REFERENCIAS
1. Redlich, O., Kister, A. T. 1948, Ind. Eng. Chem., 40, 345. [ Links ]
2. Nomoto, O. 1953, J. Chem. Phys., 21, 950. [ Links ]
3. Nomoto, O. 1958, J. Phys. Soc. Jpn. 13, 1528. [ Links ]
4. Van Dael, W. in Thermodynamic Properties and Velocity of Sound, Butterworths, 1975, London. [ Links ]
5. Ernst, S., Glinski, J., Jezowska-Trzebiatowska, B. 1979, Acta Phys. Polon., A55, 501. [ Links ]
6. Camacho, A. G., Postigo, M. A. 1998, J. Sol. Chem., 27, 719. [ Links ]
7. Canzonieri, S., Postigo, M., Salas, J., Katz, M. 2002, The Journal of the Argentine Chemical Society, 90, 31. [ Links ]
8. Mariano, A., Postigo, M., González-Salgado, D., Romaní, L. 2007, J. Chem. Thermodyn., 39, 218. [ Links ]
9. Postigo, M., Mariano, A. B., Jara, A. F., Zurakoski, N. 2009, J. Chem. & Eng. Data, 54, 1575. [ Links ]
10. Mussari, L., Canzonieri, S., Camacho, A., Tabarrozzi, R., Postigo, M. 2012, Phys. and Chem. ofLiq., 50, 530. [ Links ]
11. Awwad, A. A., Jbara, K. A., Al-Dujali, A., 1989, Fluid Phase Equilibria, 46, 259. [ Links ]
12. Franjo, C., Segade, L., Menaut, C. P., Pico, J. M., Jiménez, E. 2001, J. Sol. Chem., 30, 995. [ Links ]
13. TRC - Thermodynamic Tables Non Hydrocarbons. Thermodynamic Research Center, 1993, Texas A&M University: College Station: Tx. [ Links ]
14. Riddick, J. A., Bunger, W. B., Sakano, T. K. Organics Solvents: Physical Properties and Methods of Purification, vol. II, Fourth ed., 1986, Wiley/Interscience. [ Links ]
15. Mehta, S. K., Sharma, A. K. 2003, Fluid Phase Equilibria, 205, 37. [ Links ]
16. Suslal P., Ortega, J., de Alfonso, C., Alonso, C. 1989, J. Chem. Eng. Data, 34, 247. [ Links ]
17. Sastry N. V., George A., Jain N. J., Bahadur P. 1999, J. Chem. Eng. Data, 44, 456. [ Links ]
18. Ortega, J., Espiau, F., Toledo, R J., Dieppa, R. 2005, J. Chem. Thermodyn., 37, 967. [ Links ]
19. Mariano A. Equilibrio líquido-vapor isobárico de sistemas binarios no electrolíticos: Determinación experimental y tratamiento termodinámico. Tesis de Doctorado, Universidad Nacional de Tucumán, 2005, Tucumán. Argentina. [ Links ]












 uBio
uBio