EVALUACIÓN DEL MODELO CLIMÁTICO REGIONAL PRECIS PARA EL ÁREA DE BOLIVIA: COMPARACIÓN CON DATOS DE SUPERFICIE

EVALUARON OF THE PRECIS REGIONAL CLIMATE MODEL FOR THE REGIÓN OF BOLIVIA:

COMPARISON WITH GROUND BASED DATA

 

Marcos F. Andrade F. & Luis A. Blacutt B.

Laboratorio de Física de la Atmósfera

Instituto de Investigaciones Físicas

Universidad Mayor de San Andrés

---

RESUMEN

Los posibles efectos del cambio climático sobre regiones como Bolivia son de mucho interés tanto a nivel científico como político. Los modelos numéricos del clima tanto a nivel global como regional son una importante herramienta para el estudio de tales efectos. A fin de establecer la confiabilidad de las proyecciones de la evolución futura del clima producidas por dichos modelos es necesario, sin embargo, validar las salidas de los mismos. En este trabajo se estudia el desempeño del modelo climático regional PRECIS (Providing REgional Climatesfor Impacts Studies) del Hadley Centre de la Oficina Meteorológica del Reino Unido, sobre la región de Bolivia. La comparación de resultados del modelo con datos obser­vados en superficie a nivel mensual de temperatura y precipitación en el periodo 1961-1990 muestra que ambos parámetros tienen un buen desempeño en zonas bajas (regiones con altura menor a 500msnm) pero que sobreestima la precipitación tanto en zonas de altura intermedia (entre 500 y 3500msnm) como en la zona andina (situada a una altura mayor a 3500msnm). A su vez, la comparación muestra que el modelo subestima la temperatura (media, máxima y mínima) en las regiones con altitudes mayores a 500msnm, mientras que realiza un trabajo aceptable en las zonas bajas. Aunque la parametrizaciónde nubes y precipi­tación en las zonas de los valles y andina parece ser el elemento que más podría contribuir a las diferencias observadas, es necesario un estudio más profundo para entender los mecanismos involucrados.

Descriptores: cambio climático — Bolivia

ABSTRACT

The possible effects of climate change on regions like Bolivia are of great interest both at scientific and political lev el. Numerical climate models, both global and regional, are an important tool for studying such effects. However, in order to establish the reliability of future climate projections providedby such models is necessary to valídate its results. In this work the performance of the regional climate model PRECIS (Providing REgional Climates for Impacts Studies), developed at the Hadley Centre at the UK Met Office, is evalúated for the región of Bolivia. The comparison of temperature and precipitation of model outputs with observations taken by ground-based stations at monthly lev el for the period 1961-1990 shows that the model has a good performance for both parameters at the Bolivian lowlands (locations with an altitude below 500masl) while overestimates precipitation at regions sitúated at intermedíate heights (between 500 and 3500m asi) as well as at the Andean región (above 3500m asi). At the same time, the comparison shows that the model underestimates temperature (mean, máximum andminimum) at regions with altitudes above 500m asi, while it makes an acceptable work at the lowlands. Even though parametrization of clouds and precipitation in regions like the Altiplano and valleys is likely to contribute to the observed biases, an in depth study of the involved mechanisms is needed.

Subjectheadings: climate change — Bolivia

---

1. INTRODUCCIÓN

A raíz del incremento observado de la concentración at­mosférica de gases de efecto invernadero durante los últimos 50 años (i.e., Keeling 1960), el interés por los posibles efec­tos de este fenómeno sobre el clima futuro ha crecido enor-memente. Debido a que el clima es un sistema altamente no-lineal¹ (Palmer & Willams 2008; Andrade 2008) las he­rramientas más usadas para estudiar la evolución futura del

¹ Para una explicación más detallada ver: http://www.Ideo.columbia.edu/res/pi/arch/nonlinear.shtml

FlG. 1.— Esquema que muestra los principales controladores del clima en Bolivia.

mismo son los modelos climáticos numéricos pues estos tra­tan de representar al sistema climático de la manera más completa posible. Esto incluye no solamente a los elementos que componen este sistema como la atmósfera, los océanos o la biosfera, sino las relaciones entre éstos así como los complejos procesos de retroalimentación entre los diferentes componentes del sistema climático.

Dada la complejidad del sistema climático, los modelos numéricos todavía no pueden representar ciertos procesos de forma adecuada. Uno de los factores está relacionado a la resolución espacial del modelo y otro a la complejidad de ciertos procesos, como los relacionados con las nubes, por ejemplo. Debido a esto no queda más remedio que utilizar técnicas estadísticas que incorporen estos procesos a través de una representación paramétrica. A este proceso se le de­nomina "parametrización" y consiste básicamente en obte­ner valores (parámetros) que representen los procesos com­plejos o no resueltos a la escala en la que trabaja el modelo y permiten incorporar los efectos de los procesos físicos en las variables que el modelo resuelve (Peixoto & Ort 2002). En ese sentido la parametrización reemplaza procesos físicos por representaciones sencillas y, muchas veces empíricas, de los mismos. Por esa misma razón las parametrizaciones son típicamente las fuentes más importantes de error en los mo­delos (Palmer & Willams 2008).

La mayor parte de los modelos utilizados para el estudio del clima futuro son los denominados Modelos de Circu­lación General (GCM por sus siglas en inglés). Estos mode­los resuelven las ecuaciones que gobiernan a la atmósfera, el océano y otros componentes relevantes representados por el modelo, dividiendo el espacio en "cajas" o rejillas discretas (CCSP 2008). Por razones practicas, el tamaño de estas cajas no puede ser muy pequeño pues el tiempo de cálculo crece rápidamente conforme el tamaño de la rejilla decrece (o, equivalentemente, la resolución del modelo se incrementa). Los GCMs típicamente tienen una resolución horizontal de unos 150 a 300km² (Vera et al. 2006) y entre 18 a 56 ni­veles verticales (que van desde la superficie hasta O.lhPa). Esta resolución es suficiente para resolver fenómenos a es­cala planetaria o sinóptica pero claramente no es adecuada para estudiar fenómenos a escala regional o local. Aún más, muchos fenómenos climáticos dependen decisivamente de la orografía por lo que regiones con gradientes altitudina-les abruptos, como sucede en una parte importante del te­rritorio boliviano, están inadecuadamente representadas por los GCMs. Estas debilidades llevaron de manera natural al desarrollo de los denominados Modelos Climáticos Regio­nales (RCM por sus siglas en inglés). Estos son modelos que operan en un dominio mucho menor que los GCMs y a una resolución mucho mayor a los mismos. A la fecha estos mo­delos pueden llegar a una resolución de kilómetros aunque típicamente trabajan entre 10 y 50 km de resolución horizon­tal. Los RCMs se relacionan con los GCMs a través de los bordes del dominio elegido pues las condiciones de borde son impuestas por los GCMs para asegurar consistencia ge­neral (global).

A pesar de los avances en la representación de los sistemas y procesos involucrados en el sistema climático, los modelos numéricos, sean estos GCMs o RCMs, deben ser evaluados a fin de establecer cuan bien representan la realidad. Este proceso, denominado comúnmente validación, se lo realiza a través de la comparación de observaciones y datos modela­dos en periodos largos que permitan definir la climatología de la región de estudio y estudiar características de la misma en la región de interés. La World Meteorological Organi-zation (WMO) recomienda un periodo mínimo de 30 años para fines de estudiar el clima (WMO 1984). En particular, el periodo 1961-1990 fue adoptado por la WMO como el periodo de referencia estándar para la estimación de las nor­males climáticas. Adicionalmente, la validación busca verifi­car que el modelo sea capaz de reproducir eventos extremos, como periodos de sequías e inundaciones, así como otros in­dicadores estadísticos que describan el clima en el periodo de estudio.

El presente trabajo muestra resultados de la validación del modelo de escala regional PRECIS aplicado a la región de Bolivia. El documento se halla estructurado como sigue: una descripción del clima de Bolivia es dada en la sección 2, los datos así como el modelo usados en este trabajo son descri­tos en la sección 3, resultados de la comparación de los datos generados por el modelo y los datos observados son descri­tos en la sección 4 mientras que la discusión es descrita en la sección 5 y las conclusiones finales son expuestas en la sección 6.

2.  CARACTERÍSTICAS Y ELEMENTOS DEL CLIMA EN BOLIVIA

El territorio boliviano se halla comprendido entre los 9°S y 23°S de latitud y 70°O y 57°0 de longitud. El clima en Bolivia está fuertemente influenciado por su ubicación

² Aunque el modelo japonés JMA-GSM (Mizuta et al. 2006) ha sido per­feccionado para correr globalmente a 20 km de resolución espacial y 6 mi­nutos de resolución temporal.

FlG. 2.— Distribución espacial de las estaciones usadas en el pre­sente estudio (ver Tabla 1). Los colores de fondo representan la ele­vación de la superficie en el territorio boliviano con base a datos obte­nidos en http: //www. ngdc .noaa.gov a una resolución de 5' de grado. Los círculos indican la localización de las estaciones usadas para el periodo 1961-1990. Los círculos blancos muestran estaciones con datos de precipi­tación solamente mientras que los amarillos indican la existencia de datos de temperatura y precipitación (color online).

geográfica, su orografía y su geomorfología. Debido a su ubicación tropical los cambios en temperatura no presen­tan grandes variaciones temporales, asimismo las fluctuacio­nes en presión son pequeñas (~ lOhPa) comparadas con las que ocurren en medias latitudes (Saucier 2003). La orografía también juega un papel importante en el clima de Bolivia pues temperatura y precipitación dependen fuertemente de la distribución altitudinal de su territorio. Casi dos tercios de Bolivia, 60% aproximadamente, se halla en regiones con al­turas menores a 500 msnm, 24% del territorio se encuentra entre 500 y 3500msnm y el restante 16% por encima de esa altura en la zona Andina (ver Fig. 2). La parte baja se puede dividir en por lo menos dos regiones: una húmeda con mu­cha precipitación, ligada a la región amazónica y otra mucho más seca en la zona denominada Chaco alrededor de 20 °S. La región de altura intermedia se caracteriza por tener un alto gradiente altitudinal que produce una alta precipitación por convección orográfica en la zona. En esta área se hallan re­giones con la más altabiodiversidad del planeta (Ibish 2008). Las zonas altas, en contraste, son regiones con baja precipi­tación y bajas temperaturas.

La precipitación en Bolivia depende fuertemente del trans­porte de humedad desde el área amazónica y/o atlántica (Ma-rengo et al. 2004). Este transporte es máximo durante la época de lluvias, típicamente entre Diciembre y Marzo, y se inhibe casi por completo en época seca. Durante la época de lluvias, el denominado monzón sudamericano (SAMS, South American Monsoon System por sus siglas en inglés) controla ese transporte de humedad. Esta última es generada hacia la atmósfera gracias a la intensa actividad convectiva en la zona central-oeste del Brasil y posteriormente transportada hacia Bolivia por los vientos alisios (Marengo et al. 2004). Debido a que la cordillera de los Andes actúa como una formidable

FlG. 3.— Dominio usado para la corrida descrita en el presente trabajo. La altura de la superficie, tal como es representada por el modelo, es también graneada.

barrera debido a su altura y gran gradiente altitudinal (ver Fig. 3), el viento proveniente del este o bien se desvía hacia el sur o es forzado a elevarse hacia los valles y la zona an­dina dejando en el camino la humedad trasportada en forma de lluvia (Marengo et al. 2002). Este comportamiento está modulado por características de escala sinóptica como la lla­mada 'Alta de Bolivia", que es un anti-ciclón estacionario ubicado a una altura aproximada de 200 hPa cuya posición varía dependiendo de la emisión de calor latente en el Ama­zonas (Lenters & Cook 1997); una región de baja presión de origen térmico en la región del Chaco; y, principalmente, por el comportamiento de la corriente en chorro de bajo nivel de Sudamérica (SALLJ, South American Low LevelJet por sus siglas en inglés) al este de los Andes. El SALLJ es una co­rriente de vientos en niveles que oscilan entre 925 y 850 hPa y que transportan humedad hacia el sureste (Vera et al. 2006) y que tiene un marcado comportamiento estacional siendo más prominente durante el verano austral y más débil en el invierno correspondiente (Marengo et al. 2002). El SALLJ alimenta la cuenca de La Plata al proveer gran cantidad de humedad a esa región. Interesantemente muy poco de esa hu­medad se precipita en la zona del Chaco boliviano (Marengo et al. 2004). La Fig. 1 muestra esquemáticamente varios de los elementos que influencian el clima en Bolivia.

En el caso del Altiplano, las épocas seca y lluviosa son muy marcadas. En verano, debido al calentamiento de la su­perficie altiplánica, se inician procesos convectivos de gran intensidad que dan origen a tormentas eléctricas de mode­rada y elevada intensidad (Garreaud 1999). Se estima que más del 80% de la precipitación total del año que ocurre en el Altiplano se da entre diciembre y marzo (Vuille 1999). En invierno, por el contrario, existe intenso flujo de aire seco desde el occidente de manera casi permanente que inhibe la precipitación casi por completo (Garreaud 1999).

Aunque todas las características sinópticas mencionadas antes están presentes la mayor parte del año, la intensidad relativa de las mismas varía a lo largo de este periodo permi­tiendo producción y transporte de humedad de una región a

TABLA 1 Lista de estaciones usadas para el periodo de estudio. Las cruces indican la existencia de datos de precipitación y/o temperatura.

otra o inhibiendo la misma. Adicionalmente, eventos como El Niño y La Niña, que son las fases positivas (calientes) y negativas (frías) de un fenómeno conocido como El Niño Southern Oscillation (ENSO, por sus siglas en inglés) modi­fican drásticamente el comportamiento climático en muchas regiones del territorio boliviano (Garreaud & Aceituno 2001, Ronchail et al. 2005).

3. DATOS Y MODELO

3.1. Observaciones de superficie

Para el presente estudio se utilizaron datos mensuales de 52 estaciones en el periodo 1961-1990. Las variables medi­das en estas estaciones fueron temperatura media, tempera­tura m ínim a, temperatura máxim a y precipitación acumulada                                          

TABLA2 Características de la corrida usada en el presente trabajo.

mensual. Los datos fueron obtenidos del Servicio Nacional de Meteorología e Hidrología de Bolivia. La distribución es­pacial de las estaciones utilizadas se muestra en la Fig. 2, donde además se incluye la elevación de superficie. La Ta­bla 1 presenta información relacionada a las estaciones usa­das en el presente trabajo. Las 52 estaciones utilizadas tenían datos de precipitación acumulada mensual en tanto que sola­mente 30 tenían registro de temperatura. En todos los casos se exigió que hubiera por lo menos el equivalente a 10 años de datos aunque los mismos no formaran series continuas de tiempo. Como se observa en la Fig. 2 es evidente que la falta de estaciones impide cubrir de manera adecuada la to­pografía de Bolivia. Existen pocas estaciones en las zonas bajas, aunque en este caso el hecho que el terreno sea relati­vamente plano alivia en algo la baja densidad de estaciones. La mayor densidad de estaciones se encuentra en los valles y en la zona altiplánica aunque con preferencia en la zona cercana a la Cordillera Oriental. Se tuvo acceso a muy pocos datos, para el periodo de estudio, en la zona de la Cordillera Occidental.

Aunque para el estudio también se tuvieron acceso a datos de otras fuentes se decidió usar solamente los datos provis­tos por el Servicio Nacional de Meteorología e Hidrología (SENAMHI) boliviano debido a que se encontraron diferen­cias, algunas de ellas significativas, entre las diferentes fuen­tes de datos. En todo caso, independientemente de cual sea la fuente de datos, el proveedor primario de los datos es SE­NAMHI por lo que el análisis de las diferencias encontradas es un tópico que merece ser investigado en otro trabajo.

Adicionalmente, se usaron datos interpolados a0.5°x0.5° lat-lon de temperatura media y precipitación obtenidos del Centerfor ClimaticResearch, University ofDelaware (Lega-tes and Willmont 1990a, 1990b). Aunque este tipo de datos permite tener una cobertura espacial y temporal muy buena del territorio objeto de estudio debe tenerse en cuenta que en aquellas regiones donde no existan datos obtenidos por estaciones de tierra los valores son típicamente interpolados y/o generados de forma sintética (Garreaud et al. 2008) por lo que se debe tener especial cuidado con la interpretación de estos datos en dichas regiones. Por esta razón en el pre­sente trabajo se usan los datos interpolados para un análisis referencial y cualitativo solamente.

3.2. El modelo climático regional PRECIS

El modelo PRECIS (Providing REgional Climates for Im-pacts Studies) forma parte de la versión del modelo de cir­culación regional británico HadRM3P (Jones et al. 2004). HadRM3P tiene 19 niveles verticales y dos posibles reso­luciones horizontales, 25 y 50km. Las condiciones de borde pueden ser elegidas de varias posibles opciones dependiendo el periodo en el cual se necesitan las simulaciones. Para el caso del periodo 1961-1990 existen resultados no solamente obtenidos de GCMs sino también de fuentes observaciona-les como los reanálisis europeo y estadounidense. La versión del modelo con la que se trabajó fue la 1.7. Como todo mo­delo climático las características de la resolución de las ecua­ciones de desenvolvimiento atmosférico suelen dividirse en dos partes, una denominada "dinámica" y otra denominada "física". En cuanto a la dinámica del modelo, éste es hi-drostático, es decir no considera de manera explícita los pro­cesos convectivos que generan nubes y por lo tanto no de­termina de manera directa la precipitación. En cuanto a la física del modelo, se recurren a parametrizaciones. Este pro­ceso se logra utilizando funciones determmísticas simples. Para los procesos como la formación de nubes y precipi­tación se utilizan parametrizaciones de acuerdo a Gregory y Morris (1996). La radiación sigue el esquema desarrollado por Edwards y Slingo (1996) y modificado por Cusack et al., (1999). Estos esquemas son fijos independientemente de las características geográficas sobre las que se corre el modelo. Para fines de la solución de las ecuaciones, los años son de 360 días y cada mes consta de 30 días.

Las ecuaciones del modelo son "dirigidas" por un modelo de escala global, las condiciones de borde lateral son incor­poradas al modelo mediante el método de relajación new-toniana (Davis & Turner 1977) en la que se estima que los primeros 400 km cercanos al borde del dominio consisten en la zona de amortiguamiento que no debe ser considerada en el análisis debido a que ésa es la zona en la que el modelo global se acopla con el modelo regional. De acuerdo a las recomendaciones de los desarrolladores del modelo, el con­torno sobre el cual se definen los bordes laterales no debería cortar cadenas montañosas y debería tener un área del orden de 5000 x 5000km² (Jones et al. 2004). La primera recomen­dación, sin embargo, es prácticamente imposible de cumplir en nuestro caso debido a las características geomorfológicas de la región de estudio. La segunda recomendación está re­lacionada al hecho que un dominio muy pequeño podría res­tringir en exceso la circulación generada por el RCM mien­tras que un dominio muy grande podría generar patrones de circulación tan diferentes a los generados por el GCM que perturbaría la circulación general modelada por este último (Jones et al. 1995; Rojas & Seth 2003). Por esta razón, se realizaron experimentos preliminares variando el tamaño del dominio para tratar de determinar el tamaño óptimo. Es­tas corridas experimentales fueron efectuadas para tres años (1960-1962) y con dominios que variaban en 800km tanto en latitud como en longitud partiendo de un área que englobaba a Bolivia (unos 1300 x 1200¿m²) hasta un área del orden de 5000 x 5000km². Los resultados de estos experimentos mostraron diferencias entre los distintos dominios. Aunque las diferencias entre un dominio y el siguiente más grande

FlG. 4.— Temperatura media mensual promedio para el periodo 1961-1990 para estaciones seleccionadas. Los puntos llenos indican el promedio de la diferencia entre datos modelados y observados en tanto que la región sombreada indica la variabilidad (±0) de esa diferencia en el periodo de estudio. La línea punteada delgada indica el valor promedio anual para el periodo de estudio mientras que la línea discontinua gruesa indica el valor referencial para cuando la diferencia modelo menos observaciones sea cero.

Se hacían, en promedio, más pequeñas, al agrandar el domi­nio no se observó una clara convergencia de los resultados ni para la precipitación ni para la temperatura.

Los resultados de los experimentos preliminares sugieren la necesidad de un estudio más detallado respecto al tamaño óptimo del dominio pero el mismo está fuera del alcance del presente trabajo. Por esta razón se optó por seguir las reco­mendaciones usuales para este modelo (Jones et al. 2004) y se definió trabajar con un dominio de 5000 x 4400^/w ². Dado el tamaño del dominio se decidió utilizar una resolución de 50km principalmente por limitaciones de recursos compu-tacionales. La Fig. 3 muestra el dominio usado además de la topografía manejada por el modelo. Además, se eligió usar el modelo global HadAM3P desarrollado por el Hadley Cen­tre (Pope et al. 2000) como condición de contorno princi­palmente por razones de consistencia con otros trabajos rea­lizados en Sudamérica (por ejemplo, Marengo et al. 2009; Soares & Marengo 2008). La Tabla 2 resume las principales características de la corrida usada en este artículo.

4. VALIDACIÓN DE LAS SALIDAS DEL MODELO

A fin de realizar la validación del modelo se corrigieron las salidas de temperatura del mismo tomando en cuenta la di­ferencia entre la altura de las retículas del modelo y la altura de cada estación. Para esta corrección se usó un gradiente térmico dc5°C/km basado en los datos observados. Estos va-lores corregidos, junto a los de precipitación, fueron interpo­lados espacialmente para una comparación "uno a uno" con los datos obtenidos en superficie para cada mes del periodo 1961-1990. Las diferencias entre datos del modelo, inter­polados espacialmente a través de una interpolación bilineal simple³, y las observaciones fueron entonces calculadas para cada variable y estación. Las series temporales resultantes muestran que en tierras bajas la diferencia promedio entre va­lores modelados y observados de temperatura media es rela­tivamente pequeña, del orden de 1 °C, aunque con variaciones individuales de hasta 5 °C. No se observa una dependencia es­tacional evidente. En tierras altas, sin embargo, se observan diferencias marcadas entre valores modelados y observados, mostrando, en algunos casos, una evidente dependencia es­tacional. En las regiones intermedias, típicamente valles, las diferencias promedio entre modelo y observaciones son no­toriamente más grandes alcanzando valores de hasta 8 °C con una fuerte variabilidad alrededor del valor medio pero sin mostrar, la mayor parte de las veces, una fuerte dependencia estacional. Un comportamiento similar se observa para las temperaturas mínimas y máximas medias mensuales.

Las Figs. 4, 5 y 6 muestran los valores promedio mensua­les de las diferencias entre valores modelados y observados para el periodo 1961-1990 para la temperatura media, tem-

³ NUMERICAL RECIPES IN C: THE ART OF SCIENTIFIC COMPU-TING, Copyright (C) 1988-1992 by Cambridge University Press.

MODELO CLIMÁTICO REGIONAL PRECIS

FlG. 5.— Lo mismo que para la Fig. 4 pero para la temperatura mínima media mensual.

peratura media mínima y la temperatura media máxima, res­pectivamente. Los gráficos muestran estas diferencias para cada mes del año. La línea punteada delgada indica el valor medio anual mientras que la línea punteada gruesa indica el valor referencial cuando la diferencia es cero. Si el modelo reprodujera las observaciones perfectamente, todos los pun­tos en estos gráficos estarían sobre la línea punteada gruesa y tendrían variabilidad nula alrededor de la misma (todas las diferencias serían igual a cero). A fin de ilustrar el compor­tamiento de la diferencia "modelo menos observaciones" se seleccionaron estaciones representativas en las regiones Al­tiplano, valles y tierras bajas para ilustrar el comportamiento típico observado en estaciones localizadas en estas regiones. En el caso de las temperaturas medias mensuales se observa (Fig. 4) que el modelo reproduce razonablemente bien el ci­clo estacional en la mayor parte de las estaciones (pues la pendiente de la diferencia es cercana a cero) pero existen di­ferencias sistemáticas importantes especialmente en la zona andina y la de los valles, donde las diferencias medias llegan hasta 7°C, mostrando que el modelo subestima la tempera­tura media en prácticamente todas las estaciones. Sin em­bargo, existen algunas estaciones, Oruro por ejemplo, donde la diferencia modelo menos observaciones exhibe una clara dependencia estacional a lo largo del año. En tierras bajas, por otro lado, la diferencia observada en las distintas estacio­nes es muy cercana a cero, como se muestra para el caso de Santa Cruz.

Para la temperatura mensual promedio mínima (Fig. 5) se observa un comportamiento similar a la temperatura media con una ligera tendencia a mostrar mayor dependencia esta­cional como se puede ver en el caso de Cochabambay Oruro. Una vez más esta diferencia es cercana a cero para las es­taciones localizadas en tierras bajas mientras que se observa que el modelo subestima la temperatura mínima en zonas por encima de 500msnm.

En el caso de la temperatura mensual promedio máxima la dependencia de la diferencia estacional de los valores mode­lados con los observados es relativamente pequeña (Fig. 6), pero la diferencia promedio anual es más grande que en el caso de la temperatura mínima y media. Una vez más la dife­rencia mensual promedio más grande ocurre en la región de los valles mientras que el modelo muestra un acuerdo bueno con las observaciones en tierras bajas.

En el caso de la precipitación (Fig. 7), los datos mues­tran un sesgo mucho más marcado entre valores modela­dos y valores observados para lugares de altura y/o con pen­diente elevada (como la región de los valles, por ejemplo). En este caso, el modelo no sólo sobreestima la precipitación en prácticamente todas las estaciones de la zona sino que la di­ferencia entre valores modelados y observados muestra una marcada dependencia estacional. La variabilidad en el pe­riodo de estudio es también bastante grande tal como lo evi­dencia la Fig. 7. Como era de esperarse, dicha variabilidad es mayor durante la época de lluvias. Interesantemente, las

FlG. 6.— Lo mismo que para la Fig. 4 pero para la temperatura máxima media mensual.

estaciones de tierras bajas muestran un acuerdo (estadístico) muy bueno entre lo predicho por el modelo y las observacio­nes. En este caso, sin embargo, es importante tomar en cuenta que a pesar que las diferencias absolutas en invierno no pa­recen ser grandes, la precipitación en esta temporada del año es baja en prácticamente todas las regiones de Bolivia.

La Fig. 8 muestra las diferencias promedio anuales para las cuatro variables en estudio para las distintas estaciones donde hay datos. Las diferencias, expresadas a través de círculos de colores, corresponden a las estaciones usadas en el análisis. Cuanto más cercanos estos valores a cero, mejor el desempeño del modelo climático. Esto sin embargo podría llevar a falsas conclusiones pues no expresa posibles depen­dencias estacionales, como en la mayoría de las estaciones de altura. El gráfico muestra que de manera sistemática, y para las cuatro variables estudiadas, los valores entregados por el modelo se hallan cercanos a los valores observados en las zonas bajas. Un análisis estación por estación muestra que el modelo también reproduce bien el comportamiento estacional en esta área. Esto sugiere que el modelo realiza un buen trabajo en dicha región. Sin embargo, en lugares donde el gradiente altitudinal es grande o en estaciones si­tuadas en lugares planos pero a gran altitud, como son las estaciones del Altiplano boliviano, la diferencia entre los va­lores modelados y medidos es relativamente grande. El mo­delo subestima sistemáticamente la temperatura tanto media como mínima y máxima. Esta diferencia no parece ser, sin embargo, dependiente de la altura. La Tabla 3 sintetiza cuan­titativamente lo expresado al mostrar, por región, los valo­res medios de las diferencias de cada variable estudiada, la correspondiente desviación estándar y la raíz cuadrática me­dia. En prácticamente todos los casos estos parámetros es­tadísticos son más pequeños para las zonas bajas que para los valles y zonas altas indicando un mejor desempeño del modelo en aquella región.

Dada la evidente falta de información en grandes regio­nes del territorio objeto de estudio se usaron datos interpo­lados espacialmente (ver sección 3.1) para tener una mejor idea del comportamiento del modelo. Es necesario, sin em­bargo, tener presente que la falta de estaciones en varias de las regiones de este territorio podrían hacer que los valores en dichas áreas sean solamente producto de la interpolación y por tanto podrían no representar adecuadamente el com­portamiento de la temperatura o precipitación en dichas re­giones. Por esa razón, las comparaciones que a continuación se presentan tienen por objeto proveer una estimación cua­litativa del comportamiento espacial promedio del modelo respecto a las estimaciones basadas en observaciones en el periodo 1961-1990.

Las Figs. 9a y 9b muestran, respectivamente, las climato­logías de la temperatura media mensual y precipitación acu­mulada anual obtenidas de los datos interpolados. Para fi­nes de claridad se han interpolado espacialmente a una ma­lla más fina aún dichos resultados y sobrepuesto los valores

FlG. 7.— Precipitación acumulada mensual para el periodo de estudio. Se muestran sólo algunas estaciones seleccionadas de las tres regiones mencionadas en el texto. Símbolos y área sombreada tienen el mismo significado que en la Fig. 4.

promedio para el periodo 1961-1990 obtenidos de las obser­vaciones de estaciones de superficie (representados por los círculos). Las figuras muestran una correspondencia razona­ble entre datos medidos y datos interpolados tanto para tem­peratura como para precipitación. Los rasgos más relevantes mostrados por los datos interpolados coinciden con carac­terísticas reportadas por el SENAMHI boliviano (Carrasco 2009, comunicación personal), por ejemplo el máximo de precipitación en la zona central de Bolivia. Las Figs. 9c y 9d muestran los valores climatológicos de temperatura y pre­cipitación, respectivamente, pero obtenidos por PRECIS. En estos gráficos también se presentan los valores provenien­tes de las estaciones de superficie y se mantienen las esca­las de colores como en 9a y 9b a fin de facilitar la compa­ración con los valores "observados". Los gráficos muestran que los datos modelados de temperatura reproducen cualita­tivamente bien los datos observados pues las zonas frías y calientes están adecuadamente representadas en términos es­paciales. Por el contrario, en el caso de la precipitación se ob­serva que el modelo produce excesiva precipitación en toda la zona de fuerte gradiente altitudinal y falla en reproducir el máximo observado de precipitación centrado aproximada­mente en 64°0 y \6°S. Para poder comparar de mejor ma­nera estas diferencias se calcularon los valores "modelo me­nos observaciones" (Figs. 8e y 8f). Estas diferencias indican que las temperaturas (Fig. 8e) están en general razonable­mente modeladas (comparadas con los datos interpolados) aunque en gran parte del territorio boliviano se observa sub­estimación de las mismas. Por otro lado, aunque el modelo reproduce razonablemente bien la distribución espacial de la precipitación, en el sentido que reproduce adecuadamente el hecho que exista mayor precipitación en zonas bajas que en zonas altas, muestra una fuerte sobreestimación en la región de los valles. A pesar de eso, en una parte importante del área de interés la diferencia entre modelo y observaciones es menor a 500mm/año (en valor absoluto).

5.  DISCUSIÓN

La comparación de datos de superficie con las salidas del modelo muestra que éste realiza un buen trabajo en zonas bajas al reproducir razonablemente bien valores mensuales de temperatura media, mínima y máxima, así como la pre­cipitación acumulada mensual. Por el contrario, en lugares donde la pendiente es elevada o la altura de superficie es alta el modelo subestima de manera sistemática la temperatura y sobreestima la precipitación. La variable que es mejor esti­mada por el modelo es la temperatura mínima mientras que la temperatura máxima es la que más pobre desempeño tiene en el grupo de las temperaturas. En el caso de la precipi­tación, se observa un aceptable desempeño del modelo en la región de tierras bajas. En esta zona, la mayor parte de los va­lores modelados se hallan dispersos alrededor de los valores observados. En la región de valles, por el contrario, se ob­serva una marcada sobreestimación de la precipitación a casi

FlG. 8.— Valores anuales promedio, para el caso de las temperaturas (a,b y c), y acumulados anualmente (d), para el caso de la precipitación, de las diferencias "modelo menos observaciones". Los colores de fondo representan la variación de altura del terreno respecto a nivel del mar. Los círculos de colores muestran las diferencias de las variables meteorológicas estudiadas para las diferentes estaciones usadas en el presente estudio. Nótese las distintas escalas en todos los gráficos (color online).

cualquier altura. Del mismo modo, en la región altiplánica se observa una elevada sobreestimación de la precipitación. A pesar de este hecho, el modelo es capaz de reproducir el ciclo estacional produciendo mucha más lluvia en la estación húmeda que en la época seca como se espera. El buen com­portamiento mostrado por el modelo en tierras bajas, sin em­bargo, debe ser analizado con cuidado. Una comparación a escala continental (Marengo et al. 2009) muestra que el mo­delo subestima la precipitación en regiones al este y noreste de la región de estudio en el presente trabajo. Esto podría in­dicar que el buen acuerdo entre modelo y observaciones en las regiones bajas podría, al menos en parte, deberse a que esta región se encuentra en la zona de transición entre sub y sobreestimación. Es necesario un estudio más profundo que permita entender las causas de estos sesgos para asegurar que el modelo realiza un buen trabajo por las causas correctas.

El modelado de los parámetros meteorológicos sobre Boli-via no es trivial. En primer lugar porque este país se encuen­tra en la región tropical, segundo porque su territorio posee elevados gradientes altitudinales y tercero porque no existe la suficiente cantidad de información de superficie o de ni­veles de altura que permitan afinar adecuadamente los pro­cesos parametrizados en el modelo y/o validar los resultados de los mismos. En nuestro caso, si bien el modelo realiza un trabajo aceptable en cuanto al parámetro de temperatura, produce desviaciones importantes respecto a los valores ob­servados en el caso de la precipitación, especialmente en re­giones con fuerte gradiente altitudinal. La causa de estas di­ferencias podría deberse, al menos en parte, al hecho de que el modelo utiliza un sólo esquema de parametrización para la convección para todo el dominio (Jones et al., 2004). Los procesos convectivos son diferentes en zonas bajas compara­dos a los sistemas en tierras altas, siendo los sistemas con­vectivos de mesoescala los mayores aportantes a la lluvia en las tierras bajas (Halverson et al. 2002; Lang & Barros 2004). Como la parametrización es única para una región con oro­grafía tan variada, es difícil que el modelo represente adecua­damente ambos procesos simultáneamente. De hecho el es­tudio de las parametrizaciones para el Altiplano es un tópico pendiente de investigación. Adicionalmente, la pobre reso­lución de la orografía de la región (a una resolución de 50 km es posible tener variaciones de 1800/w de altura entre puntos de retícula adyacentes) podría también contribuir a los sesgos observados. Comparaciones hechas entre corridas realizadas a 25 y 50 km de resolución con PRECIS (Seiler 2009) mues­tran, sin embargo, diferencias relativamente menores entre

FlG. 9.— Comparación de los resultados entregados por el modelo con datos de superficie interpolados espacialmente. Estos valores, a una resolución original del orden de 50km, fueron interpolados a una malla mucho más fina para fines de claridad. Las figuras (a) y (b) muestran la climatología de los datos observados para el periodo 1961-1990, mientras las figuras (c) y (d) muestran los valores climatológicos de los datos modelados para el mismo periodo. Las figuras (e) y (f) muestran la diferencia de (c)-(a) y (d)-(b), respectivamente. Los círculos muestran los valores climatológicos de las observaciones obtenidas de las estaciones de superficie (color online).

Por último es bueno mencionar que en el contexto del cam­bio climático se espera que ocurran cambios en las distribu-ciones de precipitación así como incremento o decremento de eventos extremos (IPCC 2007). Por eso la capacidad del modelo de reproducir eventos que afectan al territorio boli­viano como inundaciones, sequías y heladas, por ejemplo, debe ser evaluada. Una inadecuada parametrización o una pobre representación de la orografía regional no explican los resultados de ambas corridas. En todo caso, resultados de otros modelos también muestran sobreestimación de la precipitación sobre zonas de fuertes gradientes altitudinales (Solmanetal. 2007).

TABLA3

Resultados del análisis estadístico realizado para todas las estaciones dentro de

cada una de las regiones definidas en el texto.

completamente las diferencias observadas. Por esa razón, un análisis de variables de altura como vientos, transporte de humedad asociado y otros parámetros que permitan evaluar cuan bien reproduce el modelo las características regiona­les que controlan el clima en Bolivia es también recomen­dable. Un estudio más profundo podría permitir mejorar el desempeño del modelo sobre Bolivia.

6.  CONCLUSIONES FINALES

La comparación de resultados del modelo con datos obser­vados en superficie a nivel mensual de temperatura y preci­pitación en el periodo 1961-1990 indica que el modelo tiene un buen desempeño en zonas bajas (menos de 500msnm). Sin embargo, en zonas de altura intermedia (entre 500 y 3500msnm) y zonas altas (altura mayor a 3500 msnm) el mo­delo subestima, en algunos casos fuertemente, tanto tempe­ratura media y temperatura máxima. La temperatura mínima también es subestimada en estas regiones pero en menor ma­nera que las otras dos variables de temperatura. En todo caso, la temperatura mínima es la variable mejor modelada por PRECES para Bolivia. Con respecto a la precipitación se ob­serva una sobreestimación para las regiones con altura ma­yor a 500m pero un comportamiento aceptable para alturas menores. La sobreestimación más fuerte se da en la región con el gradiente altitudinal más grande. Estos resultados son corroborados a través de una comparación de los datos entre­gados por el modelo contra datos de superficie interpolados espacialmente. En este caso se observa claramente que las mayores diferencias se producen en las regiones de gran gra­diente altitudinal. En las otras regiones, tierras bajas y parte del altiplano, las diferencias son relativamente menores.

AGRADECIMIENTOS

El presente trabajo contó con el apoyo de Conservation International, oficina regional Bolivia, y la colaboración del Servicio Nacional de Meteorología e Hidrología de Bolivia (SENAMHI) a través del climatólogo Gualberto Carrasco. Agradecemos también a los dos revisores por sus comenta­rios y sugerencias que permitieron hacer mucho más claro este manuscrito.

 

REFERENCIAS

1 Andrade, M. F. 2008, RBF, 14,42        [ Links ]

2 CCSP. 2008, Climate Models: An Assessment of Strengths and Limitations. AReport by the U.S. Climate Change Science Program and the Subcom-mittee on Global Change Research [Bader D.C., C. Covey, W.J. Gutowski Jr., I.M. Held, K.E. Kunkel, R.L. Miller, RT. Tokmakian and M.H. Zhang (Authors)] (Department of Energy, Office of Biological and Environmen-tal Research, Washington, D.C., US A, 124 pp)

3   Cusack, S.and Edwards, J. M. & Crowther, J. M. 1999, J. Geophys. Res., 104, n.D2, 2051        [ Links ]

4   Davies, H. C. & Turner, R. E. 1977, Q. J. R. Meteorol. Soc, 103, 225        [ Links ]

5   Edwards, J. M. & Slingo, A. 1996, J. Roy. Meteor. Soc, 122, 689        [ Links ]

6   Garreaud, R D. 1999, Mon. Wea. Rev, 127, 901        [ Links ]

7   Garreaud, R D. & Aceituno, P 2001, J. Climate, 14, 2779        [ Links ]

8 Garreaud, R. D. et al. 2008, Present-day South American climate, Paleo-geogr. Palaeoclimatol. Palaeoecol, doi: 10.1016/j.palaeo.2007.10.032        [ Links ]

9   Gregory, D. & Morris, D. 1996, Clim. Dyn., 12, n. 9, 641        [ Links ]

10  Halverson, J. B., Rickenbach, T., Roy, B., Pierce, H., & Williams, E. 2002, Monthly Weather Review, 130,1493        [ Links ]

11 Ibisch, P L., Beck, S. G., Gerkmann, B., & Carretero, A. 2008, Ecorregio-nes y ecosistemas. Pp. 47-88. en: Biodiversidad: La riqueza de Bolivia. Estado de conocimiento y conservación (P. L. Ibisch & G. Mérida, Eds.) (Ministerio de Desarrollo Sostenible. Editorial FAN. Santa Cruz de la Sie­rra, Bolivia. IUCN)        [ Links ]

12 IPCC. 2007, Climate Change 2007: Impacts, Adaptation and Vulnerability Contribution of Working Group II to the Fourth Assessment Report of the Intergovernmental Panel on Climate Change (M.L. Parry, O.F Canziani, J.P Palutikof, PJ. van der Linden and CE. Hanson, Eds.) (Cambridge University Press, Cambridge, UK, 976pp)        [ Links ]

13  Jones, R. G., Murphy, J. M., & Noguer, M. 1995, Quarterly Journal of the Royal Meteoro logical Society 121,1413        [ Links ]

14 Jones, R. G., Noguer, M., Hassell, D. C, Hudson, D., Wilson, S. S., Jenkins, G. J., &Mitchell, J.F. B. 2004, Generating high resolution climate change scenarios using PRECIS (Met Office Hadley Centre, Exeter, UK, 40pp)        [ Links ]

15 Lang, J. L. & Barros, A. P. 2004, Journal of the Meteorological Society ofJapan, 82, 829        [ Links ]

16  Legates, D. R. & Willmont, C. 1990a, Int. J. Climatol., 10, 111 —. 1990b, Theor. Appl. Climatol., 41, 11        [ Links ]

17 Lenters, J. D. & Cook, K. H. 1997, J. Atmos. Sci., 54, 656        [ Links ]

18  Marengo, J. A., Douglas, M. W., & Silva Dias, P. L. 2002, J. Geophys. Res., 107(D20), 8079, doi:10.1029/2001JD001188        [ Links ]

19 Marengo, J. A., Jones, R., Alves, L. M., & Valverde, M. C. 2009, International Journal of Climatology, 29, 2241        [ Links ]

20 Marengo, J. A., Soares,W. R., Saulo, C., & Nicolini, M. 2004, J. of Climate, 17, 2261        [ Links ]

21  Mizuta, R. et al. 2006, J. Meteor. Soc. Japan, 84, 165        [ Links ]

22 Organization, W. M. 1984, Technical Regulations, Vol. I (WMO Publication No. 49. Geneva, Switzerland)        [ Links ]

23 Palmer, T. N. & Williams, P. D. 2008, Phil. Trans. R. Soc. A, 366, 2421        [ Links ]

24 Peixoto & Ort. 1992, Physics of Climate (Springer-Verlag)        [ Links ]

25 Pope, V. D., Gallani, M. L., Rowntree, P. R., & Stratton, R. A. 2000, ClimateDynamics, 16, 123        [ Links ]

26 Rojas, M. & Seth, A. 2003, Journal of Climate, 16, 2454        [ Links ]

27 Ronchail, J. et al. 2005, Journal of Hydrology, 302, 223        [ Links ]

28 Saucier, W. J. 2003, Principles of Meteorological Analysis (Dover Phoenix Editions)        [ Links ]

29 Seiler. 2009, http://precis.metoffice.com/docs/PRECIS Christian Seiler FAN Bolivia v1 2.pdf        [ Links ]

30 Soares, W. & Marengo, J. A. 2008, Assessments of moisture fluxes east of the Andes in South America in a global warming scenario (DOI:10.1002/joc.1800)        [ Links ]

31 Solman, S. A., Nu˜nez, M. N., et al. 2007, Clim. Dyn., 30, 533        [ Links ]

32 Vera, C. et al. 2006, J. Climate, 19, 4977        [ Links ]

33 Vuille, M. 1999, International Journal of Climatology, 19, 1579        [ Links ]^rND^nAndrade^sM. F.^rND^sBader^nD.C.^rND^nC.^sCovey^rND^nW.J.^sGutowski Jr.^rND^nI.M.^sHeld^rND^nK.E.^sKunkel^rND^nR.L.^sMiller^rND^nRT.^sTokmakian^rND^nM.H.^sZhang^rND^sCusack^nS.^rND^sEdwards^nJ. M.^rND^sCrowther^nJ. M.^rND^nDavies^sH. C.^rND^nTurne^sr, R. E.^rND^sEdwards^nJ. M.^rND^sSlingo^nA.^rND^sGarreaud^nR D.^rND^sGarreaud^nR D.^rND^sAceituno^nP^rND^sGregory^nD.^rND^sMorris^nD.^rND^sHalverson^nJ. B.^rND^sRickenbach^nT.^rND^sRoy^nB.^rND^sPierce^nH.^rND^sWilliams^nE.^rND^sIbisch^nP L.^rND^sBeck^nS. G.^rND^sGerkmann^nB.^rND^sCarretero^nA.^rND^sJones^nR. G.^rND^sMurphy^nJ. M.^rND^sNoguer^nM.^rND^sJones^nR. G.^rND^sNoguer^nM.^rND^sHassell^nD. C^rND^sHudson^nD.^rND^sWilson^nS. S.^rND^sJenkins^nG. J.^rND^sMitchell^nJ.F. B.^rND^sLang^nJ. L.^rND^sBarros^nA. P.^rND^sLegates^nD. R.^rND^sWillmont^nC.^rND^sLenters^nJ. D^rND^sCook^nK. H.^rND^sMarengo^nJ. A.^rND^sDouglas^nM. W.^rND^sSilva Dias^nP. L.^rND^sMarengo^nJ. A.^rND^sJones^nR.^rND^sAlves^nL. M.^rND^sValverde^nM. C.^rND^sMarengo^nJ. A.^rND^sSoares^nW. R.^rND^sSaulo^nC.^rND^sNicolini^nM.^rND^sMizuta^nR.^rND^sPalmer^nT. N.^rND^sWilliams^nP. D.^rND^sPope^nV. D.^rND^sGallani^nM. L.^rND^sRowntree^nP. R.^rND^sStratton^nR. A.^rND^nMarcelo J.^sLucano^rND^nI van E.^sFuentes M.^rND^nMarcelo J.^sLucano^rND^nI van E.^sFuentes M.^rND^nMarcelo J^sLucano^rND^nI van E^sFuentes M.

EVALUACIÓN DEL POTENCIAL DE RADIACIÓN SOLAR GLOBAL EN EL DEPARTAMENTO DE COCHABAMBA UTILIZANDO MODELOS DE SISTEMAS DE INFORMACIÓN GEOGRÁFICA E IMÁGENES SATELITALES

EVALUATION OF THE GLOBAL SOLAR RADIATION POTENTIAL IN THE DEPARTMENT OF COCHABAMBA (BOLIVIA) USING MODELS OF GEOGRAPHIC INFORMATION SYSTEMS AND SATELLITE IMAGES

Marcelo J. Lucano^ & I van E. Fuentes M.t

Departamento de Física

Universidad Mayor de San Simón

---

RESUMEN

En este trabajo se estimaron los valores de la radiación solar global por medio de modelos de Sistemas de Información Geográfica e imágenes satelitales obtenidos a través de la metodología SSE de la NASA para un periodo de registros de 22 años. Con estos valores de radiación, se obtuvo la distribución temporal y espacial de la radiación solar para el Departamento de Cochabamba mediante un proceso de interpolación que utiliza el paquete de análisis geoestadístico ILWIS, considerando datos de una rejilla conformada por 16 casillas que abarcan el departamento; se utilizó el método de superficie móvil con distancia inversa, ex­ponente de peso 1, distancia esférica y segundo grado parabólico. Se observó que los niveles de radiación más bajos corresponden a los meses de mayo a julio (invierno) y los niveles de radiación más altos corres­ponden a los meses de octubre a diciembre (primavera y verano). Asimismo, se observó que la parte noreste de Cochabamba presenta los valores más bajos de media anual de radiación global, entre 4.2 — 4.5kWh/m ² al día, ya que ésta es una zona de baja altitud sobre el nivel del mar y se caracteriza por su clima tropical y alta humedad, generando una mayor dispersión de la radiación solar, en tanto que en la zona suroeste la radiación solar aumenta, ya que en ésta se localiza la Cordillera Oriental Central con un clima seco cuyos valores varían entre 5.76.3kWh/m² al día. También se distinguen siete regiones de niveles de radiación que van aumentando de noreste a suroeste, tal como se observó en estudios anteriores. Los valores de ra­diación obtenidos mediante la interpolación fueron validados con datos medidos en superficie con un error porcentual medio anual del 10 %.Descriptores: radiación solar — tecnología con base satelital

 ABSTRACT

Using Geographic Information Systems and satellite imaging, this study estimates the global solar ra-diation valúes using models generated from data recorded over a period of 22 years and applying NASAs SSE methodology. Using the se radiation valúes and the geostatistical analysis software ILWIS the time and space distribution of solar radiation for the Department of Cochabamba was obtained. The analysis involved data from a grid made up of 16 squares that make up Cochabamba and used the method of moving sur face with inverse distance, weight exponent 1, spherical distance andparabolic second order. It is observedthat the lowest levéis of radiation corresponded with the months May to July (winter) and the highest radiation levéis with the period October to December (summer). In addition, it was noted that the northeast región of the Cochabamba showed the lowest annual radiation valúes (4.2— A.5kWh/m² per day). This is due to the fact that the región is closer to sea lev el and characterised by a tropical and humid climate which leads to a greater dispersión of solar radiation. In the southwest región of Cochabamba which forms part of the Central Eastern Mountain Range and has a dry climate, the solar radiation is higher (5.7 — 6.3kWh/m ² per day). The study identifies seven regions of radiation levéis with increasing radiation from northeast to southwest which agree with previous studies. The radiation valúes obtained through interpolation were valídate d with surface measurements with an average anual error of 10%.Subject headings: solar radiation — satellite related technologyTEmail:   cclimaticos@fcyt.imiss.edu.bo.
 
 

---

1. INTRODUCCIÓN

A medida que la demanda de energía renovable crece, así lo hace la necesidad de fuentes de datos más precisos de estas energías. Sin embargo, en Bolivia, así como en muchos otros países, relativamente pocas estaciones meteorológicas colec­tan datos de radiación solar requeridas para conocer el poten­cial y el desempeño de sistemas de energía solar y en parti­cular de sistemas fotovoltaicos. Asimismo, las tecnologías de energía renovable están siendo usadas alrededor del mundo para suplir el uso de energía eléctrica y para desempeñar trabajo mecánico tal como: bombeo de agua, suministro de combustible para transporte, provisión de requerimientos de calentamiento y enfriamiento para el diseño de edificios, etc.Las fuentes de energía renovable, particularmente para tec­nologías solares, son fuertemente dependientes de las condi­ciones y fenómenos climatológicos y están también afecta­das por procesos microclimáticos. Debido a la ausencia de una red meteorológica de monitoreo densa y extensa, se de­ben utilizar modelos numéricos, conocimiento empírico de las características microclimáticas y observaciones indirec­tas derivadas del análisis y observaciones de datos provenien­tes de sensores remotos localizados en satélites para desarro­llar un conocimiento de las características geoespaciales así como de la extensión de estos recursos.Ya que una red de estaciones para caracterizar el régimen de radiaci ón solar en todo el país resultaría muy costosa, se han utilizado métodos indirectos para estimarla, tales como mediciones de insolación o nubosidad; pero aún la red de estaciones heliográficas y meteorológicas tiene grandes zo­nas con una cobertura deficiente, particularmente en regio­nes donde la radiación solar tiene un régimen muy diferen­ciado, como las regiones montañosas y los llanos. Desde la aparición de los satélites meteorológicos se abrió una nueva perspectiva para estimar parámetros de radiación y se han realizado estudios encaminados a ello. En los últimos 30 años la literatura especializada reporta diversos métodos de cálculo de la radiación solar, con distintos grados de comple­jidad.En este trabajo, con base en la implementación de técnicas de interpolación, se estiman los niveles de radiación solar en el Departamento de Cochabamba a partir de datos de irradiación solar obtenidos de imágenes satelitales procesa­das con la metodología SSE (Surface Meteorology and Solar E^/^)delaNASA2. REVISIÓN BIBLIOGRÁFICA2.1. Estimación de la radiación solar a partir de imágenes satelitalesDesde que se hicieron disponibles las imágenes de satélite de alta resolución en formato digital, comenzaron a aparecer estudios sobre la estimación de la radiación solar a partir de éstas. La gran ventaja de los métodos de estimación de ra­diación basados en imágenes satelitales es precisamente su resolución espacial. Con ellas es posible generar mapas de radiación solar con una resolución muy detallada (de 2 a 10 km¹) sobre regiones específicas. Esto los convierte en una
fuente de información muy adecuada, por ejemplo, para ser integrada en Sistemas de Información Geográfica (SIG).El trabajo de Gautier et al. (1980) da una pauta de la me­todología general seguida hasta la actualidad. En el trabajo mencionado se incorpora un modelo de cálculo de cierta complejidad, que requiere información del contenido de agua precipitable y al mismo tiempo incorpora el efecto de la nu­bosidad aplicando una relación lineal simple entre la brillan­tez de la nube en la imagen de satélite y su factor de ab­sorción. El método se aplica a imágenes de alta resolución (1 — 2km/pixel) y puede calcular la distribución de la ra­diación sobre grandes áreas.Mosser & Raschke (1984) utilizan las imágenes del ME-TEOSAT, cuyas características son algo diferentes de las del GOES y aplican una normalización de los valores de píxel llevándolos de su valor original al intervalo definido por los valores máximo y mínimo observados para cada píxel de la imagen en dependencia de la hora y la época del año. A par­tir de mediciones terrestres se calcula una relación entre los valores de píxel normalizados y el cociente entre la radiación incidente y la radiación máxima (ante cielo despejado), esta relación depende además del ángulo cenital del sol y también presenta un estudio acerca del efecto que tiene el número de imágenes empleadas a lo largo del día sobre la exactitud de las sumas diarias calculadas.Según Rigollier et al. (2002) en la serie de métodos pu­blicados en los años 90 como HELIOSAT, se aplica un mo­delo normalizado tanto para los valores de píxel ante cielo despejado como para los de zonas nubladas. Se aplica una relación lineal al índice normalizado de los valores para las zonas nubladas, para obtener el índice de transparencia de la nubosidad. De esta manera se calcula la radiación tanto para las áreas de cielo despejado como para cielo nublado. Este método fue inicialmente publicado como HELIOSAT 1. En la segunda versión, HELIO SAT 2 se toma en cuenta el estado óptico de la atmósfera y se introduce un método de calibración de imágenes que permitiría trabajar con distintos sensores.Pérez et al. (2002a) presentan un método de cálculo que es­tima los valores de radiación ante cielo despejado mediante el uso de un modelo simplificado y a continuación determi­nan un índice de nubosidad tomado a partir de las imágenes visibles, mediante el cual se modifican los valores calcula­dos para obtener los valores definitivos de radiación. El mo­delo GL 1.0 del Centro de Prevención del Tiempo y Estu­dios Climáticos y del INPE en Brasil parte de una ecuación simplificada de transferencia radiactiva en las zonas de entre 400 — 700nm y 700 — 4000nm. Se toma como hipótesis que en este rango espectral casi no hay absorción en la atmósfera, por lo tanto el término de absorción por aerosoles se puede despreciar, de manera que la radiación se puede obtener co­nociendo el valor de la radiación extraterrestre. Hoyos et al. (2000) utilizan un método que emplea el mismo modelo de transferencia (GL 1.0) del INPE, las diferencias fundamen­tales consisten en una implementación acabada que facilita su utilización para puntos seleccionados de la imagen. Es-

FlG. 1.— (a) Distribución geográfica de la radiación de onda corta (SW) en un periodo de 8 años para el mes de julio (W /rn). (b) Distribución geográfica de la radiación de onda larga (LW) en un periodo de 8 años para el mes de julio (IV/ni) (color online; Darnell et al. —)

 FlG. 2.— Comparación de los valores de radiación del archivo GEBA y los valores obtenidos del análisis de imágenes satelitales (Darnell et al. —).

tos dos métodos no contemplan el efecto de la nubosidad ni permiten el c álculo para áreas grandes.Como cualquier estimación a partir de modelos, aquellas basadas en datos de satélite tienen una exactitud limitada. Convencionalmente se considera un error cuadrático medio entre 15 y 20 % para estas estimaciones, cuando se las com­para con mediciones llevadas a cabo por estaciones localiza­das en sitios específicos (ver por ejemplo, Beyer et al. 1996). Hay estudios que ubican este error en un valor menor. Por ejemplo, Zelenka et al. (1999) llevaron a cabo un estudio en el que llegan a la conclusión de que el error real de los métodos para obtener irradiancias a partir de datos de satélite es de alrededor del 12%. El resto del errores atribuido por los autores al hecho de que a través de las imágenes satélites se estiman promedios sobre grandes áreas de varios kilómetros cuadrados. Cuando se compara estos valores con medicio­nes en estaciones específicas, de manera natural ocurre un error cuadrático medio de alrededor del 15%, ya que los va­lores medidos por una estación no proveen un promedio de la región sino una medición en un punto con un clima es­pecífico.

A pesar de las ventajas que presenta la estimación de la irradiancia solar a partir de información satelital, no se debe menospreciar la importancia de una red terrestre que pro­vea información de un número grande de puntos de moni-toreo bien distribuidos sobre un territorio dado. Para que los métodos satelitales den resultados más precisos, es necesario calibrarlos (sintonizarlos) con datos de superficie, lo cual re­quiere de una buena cobertura de una red terrestre constituida por estaciones situadas estratégicamente.En Bolivia no se tiene referencia sobre algún trabajo que utilice la metodología de las imágenes satelitales para esti­mar los niveles de radiación solar, sin embargo, se han rea­lizado varios estudios de la distribución de la radiación so­lar, basados fundamentalmente en la dependencia de ésta con otras variables que se miden en un número grande de estaciones, como el numero de horas con brillo solar, apli­cando fórmulas empíricas de tipo Jngstróm (Birhuett 1993; PROPER-Bolivia et al. 1998).

2.2. Estimación de la radiación solar a partir de imágenes satelitales aplicando la metodología SSE de la NASAEl proyecto ESE (Earth Science Enterprise) de la NASA ha proporcionado un sistema de satélites de investigación para proveer datos importantes para el estudio del clima y proce­sos climáticos. Estos datos incluyen estimaciones en un pe­riodo largo de tiempo de cantidades meteorológicas y energía solar en la superficie de la tierra. La base de datos basados en imágenes satelitales ha mostrado ser lo suficientemente precisa para proporcionar datos de radiación solar confiables en regiones en las cuales las mediciones en superficies son muy dispersas o no existen (Whitlock et al. 2001; Pérez et al. 2002b).Como resultado del proyecto ESE surge el banco de da­tos de radiación SSE de la NASA (NASA-LARC —) que reúne un conjunto de datos que engloban parámetros meteo­rológicos usados para diseñar sistemas de energías renova­bles. No está diseñado como un substituto a las mediciones en superficie, sino como un estimado de datos de radiación para lugares en los que no existen redes de monitoreo densas (ej. áreas rurales). Debido a la resolución de las imágenes

FlG. 3.— Comparación entre los valores de radiación medidos en superficie y valores estimados a partir de imágenes satelitales para la estación de Páyeme, Suiza: (a) onda corta SW y (b) onda larga, (color online; Darnell et al. —).

FlG. 4.— (a) Distribución geográfica de los puntos en el centro de las grillas en el Departamento de Cochabamba. (b) Radiación media anual asignada a los puntos de referencia en unidades de kWh/nt al día.

satelitales da un promedio de las condiciones de la región cubierta con una resolución de 1 ° x I^o en latitud y longitud y el periodo de análisis del banco de datos es de julio de 1983 hasta noviembre de 2008 (22 años) con las imágenes obteni­das de alrededor de 200 satélites. Estos valores estimados son suficientemente precisos para realizar estudios preliminares.El sitio Web de la NASA habilita al usuario para la des­carga de datos de radiación solar mensual y anual para cual­quier localización en la Tierra. El banco de datos de la NASA se ha convertido en un paradigma para la fuente de infor­mación de radiación solar, debido a la alta calidad del mode-lamiento utilizado para generar el banco de datos, al hecho de que la metodología SSE es validada con numerosas esta­ciones en superficie y al hecho de que abarca una escala glo­bal y cubre un extenso periodo de tiempo. Sin embargo, el banco de datos es aún limitado por una perdida de resolución y no validación en áreas donde no existen datos en superfi­cie. Los procedimientos utilizados para generar el banco de datos SSE también encuentran problemas en áreas en las que se tienen interfaces oceánicas y áreas cubiertas con nieve.Los valores estimados de radiación solar son resultado del análisis de un periodo de 46 meses de la radiación de onda corta (SW) y onda larga (LW) procesados a través del algoritmo de Pinker-Laszlo (PinkerLaszlo 1992; Pin-ker et al. 1995; Darnell et al. —) dentro del programa ÑAS A/GE WEX/SRB. Las variables de entrada son las irra-diancias, la cantidad de nubes provenientes del programa ISCCP {International Satellite and Cloud Climatology Pro-gramme), el vapor de agua del programa GEOS-1 (Goddard Earth Observation Systems) con datos en intervalos de 3 ho­ras y datos de ozono obtenidos del sensor TOMS. Los valores de aerosoles y profundidad óptica de las nubes son utilizados como parámetros de afinamiento en los casos de cielo con y sin nubes. El error cuadrático medio (RMS) estimado para valores mensuales es de alrededor del 16% con una incer-tidumbre del 1% comparado a los datos obtenidos con me­diciones en superficie según el Centro Mundial de Datos de Radiación (WRDC).Las Figuras la y Ib muestran la distribución geográfica de la radiación promedio de onda corta y onda larga, respectiva­mente, en un periodo de 8 años para el mes de julio. La dis­tribución de la radiación SW es primordialmente zonal, mo­dulada por la distribución de las nubes. Los valores máximos se encuentran en el Ártico, Groenlandia y las regiones sub­tropicales del Hemisferio Norte. Los valores máximos de la radiación LW se localizan sobre amplias regiones en los trópicos con un decrecimiento gradual hacia los polos. Los valores más altos ocurren sobre áreas que exhiben tempera-



 

 FIG. 5.— Distribución mensual de la radiación solar global en el Departamento de Cochabamba (color online).
 
turas superficiales elevadas tal como los desiertos subtropi­cales y áreas con abundancia de nubes y vapor de agua.La Fig. 2 muestra un diagrama de dispersión de los datos de radiación mensuales del Archivo del Balance de Energía Global (GEBA) del Instituto Federal de Tecnología de Suiza y los correspondientes valores de radiación estimados a partir del análisis de imágenes satelitales. Se observa que gran parte de los puntos muestran una correlación lineal, en cuanto que los puntos fuera del grupo pertenecen a regiones con alta den­sidad de agua o con hielo superficial.Las Figs. 3a y 3b muestra una comparación entre los va­lores de radiación SW y LW respectivamente de medidas en superficie y los valores estimados a partir de imágenes sate­litales para la estación ubicada en Páyeme, Suiza.

3. METODOLOGÍA

Debido a la resolución de las imágenes satelitales, se ob­tiene un valor promedio de radiación para un área compren­dida entre 1 ° de latitud y 1 ° de longitud. El Departamento de Cochabamba se encuentra entre los 64° - 68° de longitud oeste y 15° - 19° de latitud sur abarcando un total de 16 gri­llas, por lo que el valor de radiación promedio corresponde al centro de la grilla considerada. Con este criterio, se asigna­ron para el centro de las 16 grillas el valor correspondiente de radiación solar de la base de datos SSE, estos datos tabulados se muestran en la Tabla 1.Con base a la Tabla 1, se obtuvo la distribución geográfica de los puntos centrales de las grillas en la región de estudio (Fig. 4).

tabla 1

Datos de radiación solar mensual y anual obtenidos a partir de imágenes satelitales para el Departamento de Cochabamba en kWh/nfü día.
   

   

FlG. 6.— Distribución anual de la radiación solar global en el Departa­mento de Cochabamba (color online).

4.  RESULTADOS

Con respecto al método de interpolación empleado para obtener los valores estimados de los niveles de radiación en el Departamento de Cochabamba se usó una metodología im-plementada en un estudio preliminar sobre los métodos de interpolación más eficaces para determinar los niveles de ra­diación solar (Mubiru et al. 2007; Lucano & Fuentes 2008) y se concluyó que el método: superficie móvil distancia in­versa con exponente de peso 1, distancia esférica y segundo grado parabólico es el método más adecuado para interpolar

           

FlG. 7.— Área de estudio dividida en ocho subáreas.datos satelitales.

Una vez establecido el método más apro­piado éste se utilizó para interpolar los valores de radiación solar global promedio mensuales para cada uno de los meses del año y el promedio anual.La Fig. 5 muestra la distribución de radiación solar global en Cochabamba para los doce meses del año.Se observa de la Fig. 5 que los niveles de radiación más ba­jos corresponden a los meses de mayo, junio y julio, que per­tenecen a la estación de invierno, y los niveles de radiación más altos corresponden a los meses de octubre, noviembre y diciembre, que corresponden a las estaciones de primavera y verano.La Fig. 6 muestra la distribución de radiación solar global anual para el Departamento de Cochabamba.Se observa de la Fig. 6 que la parte noreste del Departa-


        

FlG. 8.— Comparación de los valores simulados (metodología SSE) y medidos experimentalmente de intensidad de radiación solar global para el Depar­tamento de Cochabamba

FlG. 9.— Comparación de datos de radiación solar interpolados (mapa) y medidos en superficie para la estación de monitoreo en la UMSS.

mentó de Cochabamba presenta los valores más bajos de me­dia anual de radiación global, entre 4,2 y 4,5 kWh/m ² al día, debido a que ésta región es una zona de baja altitud sobre el nivel del mar y se caracteriza por su clima tropical y alta hu­medad generando una mayor dispersión de la radiación solar. En la zona suroeste la radiación solar aumenta ya que en esta región se localiza la Cordillera Oriental Central con un clima seco con valores entre 5,7 y 6,3kWh/m² al día. Asimismo, se distinguen seis regiones de niveles de radiación que van aumentando de noreste a suroeste, tendencia igualmente ob-servada en el estudio realizado por Birhuett (1993) para la obtención de los mapas de radiación solar para Bolivia.4.1. Validación de los valores de radiación interpoladosPara la validación de los datos interpolados se realizó un estudio comparativo y de validación entre los valores de ra­diación medidos experimentalmente y aquellos estimados por la NASA para el Departamento de Cochabamba (para el área entre 64° - 67° de longitud y 16° - 19° de latitud) empleando un programa elaborado en MATLAB. La Fig. 7

 
TABLA2 Comparación entre los valores de radiación global interpolados (mapa) y medidos en superficie PARA EL MISMO PUNTO DE VALIDACIÓN (Wh/m²a\ día).

 

 
muestra la división del área de estudio (Departamento de Co-chabamba) en ocho subáreas en las que se compararon los datos.Los datos experimentales fueron proporcionados por la red SENAMHI y la Fig. 8 muestra la comparación de estos con los datos simulados a través de las imágenes satelitales para un periodo de un año.Se observa que la variación temporal de los valores de radiación tanto simulados como experimentales siguen el mismo comportamiento, hecho que fue observado en la es­tación de Suiza (Fig. 3) en un trabajo similar (Darnell et al. —), excepto en los meses de enero a marzo, esto debido a que la cantidad de nubes presentes en esos meses afecta el análisis de las imágenes adquiridas.Además de la validación en las ocho sub-áreas, los valo­res de radiación solar global de los mapas obtenidos por el método de interpolación se contrastaron con datos medidos en superficie en un periodo de un año en dos estaciones remo­tas de la red SENAMHI: Aiquile (Latitud: 18.1833S, longi­tud: 65.1833W) e Independencia (Latitud: 17.3117S, longi­tud: 66.8481W); asimismo, se comparáronlos valores simu­lados con los obtenidos con un Piranómetro Kipp & Zonen Clase 2 instalado en el Departamento de Física de la Facul­tad de Ciencias y Tecnología (latitud: 17.3928S, longitud: 66.1351W) en el mismo periodo de un año (marzo 2008 -marzo 2009). La comparación entre los datos interpolados y experimentales para el mismo punto de validación y el co­rrespondiente error se muestran en la Tabla 2.La Fig. 9 muestra la variación anual de los datos de ra­diación mensual correspondientes al punto de monitoreo de la UMSS.Se observa que los valores medidos en superficie son ma­yores que aquellos obtenidos en el mapa solar en el caso de las estaciones de la UMSS y Aiquile en cuanto que lo con­trario sucede en el caso de la estación de Independencia. El error medio anual porcentual de todas las estaciones de mo­nitoreo es de 10%.

5. CONCLUSIONES

En el presente trabajo, se han utilizado los datos de ra­diación solar de la NASA obtenidos utilizando la metodo­logía SSE (NASA-LARC —) para estimar los valores de ra­diación solar global mensual y anual para el Departamento de Cochabamba. Se utilizaron los datos obtenidos a partir del análisis de imágenes satelitales para estimar la distribución de la radiación solar global, asimismo se realizó un proceso de validación con datos medidos de tres estaciones en su­perficie (UMSS, Aiquile e Independencia) obteniéndose un error medio porcentual de 10%.De acuerdo a los resultados obtenidos, se observa en la Fig. 6 siete regiones con marcada diferencia de niveles de radiación solar anual: la región con mayor cantidad de ra­diación corresponde a la zona de la Cordillera Oriental en la que los valores de radiación oscilan entre 5,4 — 7,2kWh/m² al día, la zona del trópico central con valores entre 4,2 — 4,5kWh/m² al día y la zona restante del trópico con niveles de radiación entre 4,5 — 5, AkWh/m¹ al día.El periodo de registros analizados es de 22 años (Tabla 1). La variación mensual y espacial de los niveles de radiación se obtuvo utilizando el paquete de análisis geoestadístico IL-WIS y aplicando el método de superficie móvil con distancia inversa, exponente de peso 1, distancia esférica y segundo grado parabólico. La aplicación del método de interpolación y los valores estimados muestran que en la estación de in­vierno (mayo - julio) se registra la menor cantidad de ra­diación solar, mientras que en las estaciones de primavera y verano (octubre - diciembre) se registra la mayor cantidad de radiación solar.Por otro lado, las diferencias que eventualmente pueden ser encontradas entre los valores estimados y medidos en superficie pueden ser debidas al hecho de que los valores medidos en superficie corresponden a la localización del punto de monitoreo con características geográficas y clima­tológicas particulares, en cuanto que los datos obtenidos por los satélites abarcan extensiones entre I^o x I^o, que represen- tan una media de condiciones climáticas diferentes.El método de cálculo de la radiación solar global a par­tir de imágenes satelitales desarrollado ha obtenido resulta­dos comparables a otros revisados en la bibliografía (Myers 2003; Lefevre & Diabaté 2007). Es recomendable que en lo sucesivo los valores estimados por métodos indirectos se comparen con datos registrados en un mayor número de estaciones meteorológicas para asegurar una cobertura geográfica suficiente del departamento.Asimismo, es importante incorporar las bases de datos de radiación ya sea medidas en superficie u obtenidas a través de métodos indirectos a los Sistemas de Información Geográfica (SIG), que ofrezcan a aquellos que requieren de estos datos las herramientas diversas relacionadas con el recurso solar. Esto para la evaluación de los niveles de radiación solar para cualquier localización geográfica del país, a partir de mode­los bien calibrados respecto a estos datos.También se deben incluir herramientas que permitan es­timar el rendimiento de diferentes dispositivos y/o sis­temas que utilizan el recurso solar. Este tipo de herra­mientas ya se han desarrollado en otros países (http://xn-energiasolarespaa-uxb.net) y constituyen un factor decisivo para el impulso a las energías renovables. En particular, es­tas herramientas permiten la evaluación con un grado mucho mayor de certidumbre de la viabilidad económica de proyec­tos de energía solar, facilitando el proceso de su financiación.

REFERENCIAS

1,- Beyer, H. G., Costanzo, C., & Heinemann, D. 1996, Solar Energy, 56, 207.        [ Links ]

2.- Birhuett, E. 1993, Revista E&D No. 3 PROPER Cochabamba, Bolivia.        [ Links ]

3.- Darnell, W. L. et al. —, Surface Radiation Budget: A Long-term Global Dataset of Shortwave and Longwave Fluxes http://www.agu.org/eos elec/95206e.html

4.- Gautier, C., Diak, G., & Masse, S. 1980, Journal of Applied Meteorology, 19 No. 8, 1005.        [ Links ]

5.- Hoyos, D., Cadena, C., & Su´arez, H. 2000, Revista Averma, 4 No. 8, http://g.unsa.edu.ar/asades/actas2000/08-23.html http://www.asrc.cestm.albany.edu/perez/strength.html        [ Links ]

6.- Lefevre, M. & Diabat´e, W. L. 2007, Solar Energy, 81, 240.        [ Links ]

7.- Lucano, M. J. & Fuentes, I. E. 2008, Revista Cient´ıfica Facultad de Ciencias y Tecnolog´ıa, 8.        [ Links ]

8.- Mosser, W. & Raschke, E. 1984, Journal of Climate and Applied Meteorology, 23, 166.        [ Links ]

9.- Mubiru, J. et al. 2007, Theor. Appl. Climatol., 88, 259.        [ Links ]

10.- Myers, D. R. 2003, Solar Radiation Modeling and Measurements for Renewable Energy Applications: Data and Model Quality (International Expert
Conference on Mathematical Modeling of Solar Radiation and Daylight Edinburgh, Scotland, September 15–16 ).

11.- NASA-LARC. —, http://eosweb.larc.nasa.gov/sse.

12.- P´erez, R., Incichen, P., Moore, K., Kmiecik, M., Chain, C., George, R., & Vignola, F. 2002a, Solar Energy, 73, No. 5, 307.        [ Links ]

13.- P´erez, R., Moore, K., Kmiecik, M., Chain, C., Ineichen, P., George, R., & Vignola, F. 2002b, Proc. SOLAR 2002, Sunrise on the Reliable Energy
Economy, Amer. Solar Energy Soc.

14.- Pinker, R. T. & Laszlo, I. 1992, J. Appl. Meteorol., 31, 194.        [ Links ]

15.- Pinker, R. T., Laszlo, I., Whitlock, C. H., & Charlock, T. P. 1995, Eos, 76, 145.        [ Links ]

16.- PROPER-Bolivia et al. 1998, Mapa de distribuci´on de la Energ´ıa Solar en Bolivia, Vice-Ministerio de Energ´ıa e Hidrocarburos. Programa para la
Difusi´on de Energ´ıas Renovables PROPER Bolivia – GTZ – ESMAP – Banco Mundial.

17.- Rigollier, C., Lef`evre, M., Cros, S., & Wald, L. 2002, Heliosat 2: An improved method for the mapping of the solar radiation from METEOSAT
imagery (Proceedings of the 2002 EUMETSAT Meteorological Satellite Conference. http://www.eumetsat.de/en/index.html).

18.- Whitlock, C. H., Brown, D. E., Chandler, W. S., DiPasquale, R. C., Gupta, S. K., Wilber, A. C., Ritchey, N. A., Kratz, D. P., & Stackhouse, P. W.
2001, J. of Solar Energy Engineering, Amer. Soc. Mech. Engr., 23, 211.

19.- Zelenka, A., Perez, R., Seals, R.,& Renn´e, D. 1999, Theoretical and Applied Climatology, 62, 199.        [ Links ]^rND^sBeyer^nH. G^rND^sCostanzo^nC.^rND^sHeinemann^nD.^rND^sBirhuett^nE.^rND^sGautier^nC.^rND^sDiak^nG.^rND^sMasse^nS.^rND^sHoyos^nD.^rND^sCadena^nC.^rND^sSu´arez^nH.^rND^sLefevre^nM.^rND^sDiabat´e^nW. L^rND^sLucano^nM. J.^rND^sFuentes^nI. E.^rND^sMosser^nW.^rND^sRaschke^nE.^rND^sMubiru^nJ.^rND^sP´erez^nR.^rND^sIncichen^nP.^rND^sMoore^nK.^rND^sKmiecik^nM.^rND^sChain^nC.^rND^sGeorge^nR.^rND^sVignola^nF.^rND^sP´erez^nR.^rND^sMoore^nK.^rND^sKmiecik^nM.^rND^sChain^nC.^rND^sIneichen^nP.^rND^sGeorge^nR.^rND^sVignola^nF.^rND^sPinker^nR. T.^rND^sLaszlo^nI.^rND^sRigollier^nC.^rND^sLef`evre^nM.^rND^sCros^nS.^rND^sWald^nL.^rND^sWhitlock^nC. H.^rND^sBrown^nD. E.^rND^sChandle^nW. S.^rND^sDiPasquale^nR. C.^rND^sGupta^nS. K.^rND^sWilber^nA. C.^rND^sRitchey^nN. A.^rND^sKratz^nD. P.^rND^sStackhouse^nP. W.^rND^sZelenka^nA.^rND^sPerez^nR.^rND^sSeals^nR^rND^sRenn´e^nD.^rND^sChamani^nW.^rND^sTicona^nR.^rND^sRicaldi^nE.^rND^sChamani^nW.^rND^sTicona^nR.^rND^sRicaldi^nE.^rND^sChamani^nW^rND^sTicona^nR^rND^sRicaldi^nE

OBSERVACIÓN DE NEUTRONES SOLARES Y EFECTOS SOBRE EL CAMPO MAGNÉTICO TERRRESTRE ASOCIADOS CON LA FULGURACIÓN SOLAR DEL 2 DE NOVIEMBRE DE 2003

 

OBSERVATION OF SOLAR NEUTRONS AND THE EFFECTS ON THE EARTHS MAGNETIC FIELD ASSOCIATEDWITH THE SOLAR FLARE OF THE 2ndNOVEMBER 2003

Chamani W.¹, Ticona R.² y Ricaldi E.¹

¹ Carrera de Física

² Instituto de Investigaciones Físicas

Universidad Mayor de San Andrés

La Paz-Bolivia

---

RESUMEN

El 2 de noviembre de 2003 a las 17:03:00 (GMT) se produjo una fulguración solar que fue verificada por el satélite GOES y se registró por el Monitor de Neutrones (NM-64) a las 17:17:24 (GMT) del laboratorio de Física Cósmica en el monte Chacaltaya. En particular, se observó que la fulguración produjo la variación del campo geomagnético local (F); se produjeron variaciones de la intensidad de la componente horizontal (H), de la declinación (D) y de la componente vertical (Z). Se observaron los registros de los incrementos con respecto a los valores promedio (registrados diariamente) de dichas componentes estimados en 71 nT, 10 grados y \9nT respectivamente en el Observatorio Geomagnético de Patacamaya, así como el incremento del campo neto F estimado en 66 nT registrado por el Observatorio Geomagnético de Villa Remedios. Las duraciones de la señal de neutrones y de la señal magnética fueron aproximadamente de 40 y 54 minutos respectivamente, lo que muestra que la fulguración fue intensa y la emisión de neutrones fue de larga duración.

Descriptores: fulguración solar — neutrones solares — crochets magnéticos

ABSTRACT

On the 2ndNovember 2003 at 17:03:00 (GMT) there was a solar fiare recorded by the GOES satellite. The event was also registered at 17:17:24 (GMT) by the Neutrón Monitor (NM-64) of the Cosmic Physics Laboratory located at Mount Chacaltaya in Bolivia. The fiare produced changes in the intensity of the local geomagnetic field (F) affecting all three vector components —horizontal component (H), declination (D) and the vertical component (Z). Records of the increase in relation to average valúes of the aforementioned components were observed at 71 nT, 10 degrees and \9nT at the Geomagnetic Observatory at Patacamaya (Bolivian Altiplano) and the net increase of the F field estimated at 66nT registered by the Geomagnetic Observatory at Villa Remedios. The duration of the neutrón and magnetic signáis were between 40 and 54 minutes approximately. This demónstrates that the fiare was intense and that the emission of neutrons took place over a long period of time.

Subject headings: solar fiares — solar neutrons — magnetic crochet

---

1. INTRODUCCIÓN

El estudio y la observación de las fulguraciones solares y los efectos que produce sobre el campo geomagnético han merecido la atención de muchos científicos sobre todo a partir de las observaciones de Carrington y Hodgson en 1859, cuando encontraron una interrelación entre un crochet magnético y una fulguración solar. Las fulguraciones son los eventos más violentos y energéticos en el sistema solar, los cuales están ñsicamente relacionados con las manchas so­lares; pueden acelerar iones a altas energías. Estos eventos se producen cuando la energía magnética acumulada en la atmósfera solar, cercana a una mancha, es repentinamente liberada. Seguidamente, generan ondas electromagnéticas a lo ancho de todo el espectro, desde ondas de radio hasta fre­cuencias de rayos gamma, que son producidas por emisión sincrotónica en el campo magnético solar de la corona. Mien­tras los rayos X (RX) son generados en la atmósfera so­lar mediante el fenómeno del Bremsstrahlung, los neutro­nes son producidos por la interacción de iones acelerados con la atmósfera solar. Este tipo de eventos pueden ser ob­servados por distintos métodos como: 1) la observación de la emisión con espectro-Heliógrafos, 2) la observación del flujo de rayos X con satélites y también pueden ser recono­cidos y observados indirectamente sobre los efectos que pro­ducen en el campo geomagnético, ya que ocasionan variacio-

FlG. 1.— Incremento del flujo de rayos X detectado por el satélite GOES entre el 1 y el 3 de Noviembre. El tiempo de inicio de la fulguración X8.3 fué a las 17:03 UT. La línea roja expresa el flujo de rayos X en el rango de longitud de onda de 1.0 — 8.QÁ y la azul para el rango de 0.5 — 41 (color online).

nes y perturbaciones en sus tres componentes: la horizontal (H), la vertical (Z) y la de declinación (D), debido a que un frente de partículas cargadas provenientes de la fulguración chocan con la magnetósfera de la Tierra, produciendo su de­formación y compresión, seguidas de tormentas magnéticas en la atmósfera terrestre con un retraso de hasta algunos días. Otro de los efectos que producen son los crochets magnéticos que son variaciones magnéticas rápidas debidas a una des­viación del sistema de corriente ionosférica, donde la va­riación geomagnética en el hemisferio iluminado por el sol se intensifica por un corto tiempo; el efecto es más grande cerca del punto subsolar (zenit). Por otro lado, los neutrones solares producidos son inmunes a los campos magnéticos, lo que hace posible que puedan alcanzar la superficie de la Tierra y por lo tanto nos permitan estudiar los mecanismos por los cuales han sido acelerados. Debido al interés por estudiar y observar este tipo de fenómenos que produce el sol, en este trabajo presentamos resultados preliminares del evento de una fulguración solar producida el 2 de noviem­bre de 2003 y reportamos los efectos que ha tenido sobre el campo magnético de la Tierra. Se observa una correlación del evento entre los datos del experimento del Monitor de Neutrones 12NM-64 de Chacaltayay dos observatorios geo-magnéticos, ubicados en Patacamaya y en Villa Remedios, de la Universidad Mayor de San Andrés (UMSA).

2. LA PROPAGACIÓN DE LOS NEUTRONES SOLARES

Los neutrones producidos en una fulguración solar no son afectados por el campo magnético del sol ni por el campo magnético terrestre; pero dependiendo de su energía logran alcanzar la superficie de la Tierra antes de que decaigan durante su viaje. Por ello la probabilidad de sobrevivencia, P(E), de un neutrón es:

Donde t es su tiempo de vuelo entre el Sol y la Tierra, yes el factor de Lorentz y t = 8865, el tiempo de vida del neutrón.

FlG. 2.— El contaje registrado cada 5 minutos por el Monitor de Neutrones (12-NM64) localizado en el monte Chacaltaya, Bolivia el 2 de Noviembre de 2003. Los datos después de las 18:00 UT no fueron registrados debido a un corte de electricidad. El tiempo (inicio de la fulguración) registrado fue a horas 17:17:24 UT el cual correlaciona con el tiempo registrado por el satélite GOES. Se observa que la emisión neutrónica solar intensa máxima fue a horas 17:30:01 UT.

3.  MÉTODO DEL TIEMPO DE VUELO

Los neutrones solares no pueden viajar a la velocidad de la luz debido a que tienen masa. El tiempo de su llegada a la Tierra es más largo para neutrones de bajas energías y si existe un amplio rango de energía de los neutrones produci­dos al mismo tiempo en el Sol, entonces existe también un amplio rango de tiempos de llegada. El tiempo de retraso Át, está dado por:

Donde R es la distancia entre el Sol y la Tierra (\UA = 1.496 x \0^um), c es la velocidad de la luz y v la veloci­dad del neutrón. Combinando la ecuación (2) con la (3) se obtiene:

Entonces la energía cinética del neutrón T_n es:

 

Donde M„ es la energía de la masa en reposo del neutrón (940 MeV).

 

4.  ARREGLO EXPERIMENTAL

4.1. Monitor de Neutrones NM-64

El monitor de neutrones es un instrumento para monitorear la intensidad de los rayos cósmicos galácticos y solares. Con­siste principalmente de tres partes: el reflector, el productor y el contador. El monitor MN-64 usa polietileno como re­flector. El rol del reflector es el de rechazar los neutrones de bajas energías producidos en la atmósfera y en las sustan­cias cercanas al monitor de neutrones. El plomo que rodea al reflector es usado como productor. Un contador de BF3

<

Fig. 3.— Incremento de la componente horizontal H del campo magnético de la Tierra, el tiempo de inicio fue a horas 17:43 UT. La intensidad de campo magnético del crochet fue aproximadamente 71 nT. La tormenta magnética se identifica como un cambio abrupto de la componente H al tercer día después de la fulguración.

Fig. 4.— Decremento de la componente vertical Z del campo magnético de la Tierra que se inicia a horas 17:35 UT. La intensidad de dicha compo­nente file de 19nT.

está localizado dentro del productor. El moderador interno es usado para desacelerar neutrones hasta energías térmicas, el cual está localizado entre el contador y el productor.

4.2. Observatorio Geomagnético de Patacamaya

En este laboratorio se cuenta con un arreglo óptico-mecánico (Variógrafos La Cour), un teodolito magnético y un magnetómetro de protones. El variógrafo toma los datos de las variaciones diarias de los elementos H, D, Z del campo magnético terrestre, siendo la más sensible la componente H en latitudes muy cercanas al ecuador y menos sensible la componente Z.

4.3. Observatorio Geomagnético de Villa Remedios

Este laboratorio cuenta con un arreglo de bobinas que tra­bajan a modo Flux Gate, modelo FGE, de tres componentes X, Y, ZyF, proveniente de un magnetómetro fijo Overhauser. Los datos son registrados por un Data Logger. Los registros de este observatorio son rígidos y están sujetos a un mínimo

Fig. 5.— Incremento de la componente de declinación D del campo magnético de la Tierra registrada a horas 17:51. La intensidad de dicha com­ponente fue de 10 grados.

Fig. 6.— Variación del campo magnético neto F que se inicia a horas 17:16 UT. La intensidad del campo neto F fue de aproximadamente 66nT.

de fuentes de error, siendo la variación de la temperatura del recinto del registro la más significativa.

 

5. REGISTROS Y OBSERVACIONES

Una fulguración solar intensa ocurrió el 2 de noviembre de 2003. La emisión del flujo de rayos X blandos observa­dos por el satélite GOES (Fig. 1), comenzó a incrementarse a las 17:03 UT, alcanzó su máximo a las 17:25 UT y de­cayó a la mitad de su valor máximo a las 17:39 UT. El pico del flujo de RX fue clasificado como X8.3. La mancha solar corresponde a la región 10486, ubicada en las coordenadas S\4°, W56°. En la misma región se produjo el evento solar de neutrones el 28 de Octubre de 2003. La Fig. 2 muestra el contaje registrado cada 5 minutos por el Monitor de Neutro­nes NM-64. La emisión neutrónica comenzó a incrementarse a las 17:17:24 UT, la señal intensa alcanzó su máximo a las 17:30:01 UT, el que correlaciona con el tiempo registrado por el GOES. La duración del evento fue de aproximada­mente de 40 minutos. Las Figs. 4, 5 y 6 muestran el efecto que produce la fulguración solar sobre el campo magnético de la Tierra. Se producen variaciones respecto de los valores,

registrados diariamente, de las componentes horizontal (H), vertical (Z) y de declinación (D) del campo geomagnético por el Observatorio Geomagnético de Patacamaya. La Fig. 7 muestra la variación del campo geomagnético neto (F) regis­trado por el Observatorio Geomagnético de Villa Remedios. La Fig. 4 muestra una anomalía notable (crochet) en la com­ponente H del campo, que alcanzó su máximo a las 18:04 UT con una intensidad de 71 nT. A partir de los datos que se leen de este registro, la duración de la señal magnética fue de 54 minutos, por otro lado, la nube de plasma solar llegó apro­ximadamente un día y medio después de la fulguración. La tormenta magnética se identifica como un cambio abrupto de la componente H al tercer día después de la fulguración, en este mismo lapso de tiempo ocurre la fase de compresión y deformación de la magnetósfera terrestre. La Fig. 5 muestra el decremento de la intensidad de la componente vertical Z del campo estimada en 19 nT que se inició a horas 17:35 UT. Por el contrario, en este caso se observa un incremento de la componente de declinación D del campo estimado en 10 gra­dos, que es el ángulo formado entre el polo norte geográfico y la componente H del campo.

 

6. CONCLUSIONES

Los resultados obtenidos en este estudio permiten concluir que la fulguración solar fue intensa, de larga duración y de emisión de neutrones parecida al evento registrado el 7 de septiembre de 2005 (Ricaldi 2007). Además se ha visto que el efecto que ha producido ha sido el cambio drástico de la intensidad del campo geomagnético ocasionando los llamados crochets magnéticos o anomalías magnéticas que producen la variación diaria solar (Sq), el cual se manifestó significati­vamente en el incremento de la componente H, lo cual es de esperarse para latitudes bajas como la de Chacaltaya, cerca­nas al ecuador magnético. En el instante que ocurrió la fulgu­ración solar, el Sol estaba situado casi en el cénit sobre el ob­servatorio de Chacaltaya (292.0°E, \6.2°S, 5250m.s.n.m.), por lo tanto se encontró en una muy buena posición para la observación de los neutrones solares. El rango de energías de los neutrones solares obtenido mediante el método del tiempo de vuelo estuvo entre 50 y \94MeV, con velocidades relativistas entre 0.31cy 0.56 c. Por otro lado, se han esti­mado los incrementos y decrementos del campo neto F, las componentes D y Z del mismo en 66nT, 10 grados y \9nT, respectivamente. Se ha visto que la tormenta geomagnética se produce al tercer día después de la fulguración, la cual des­prendió una nube de plasma que tardó 1 d 12h y 46 m inutos en llegar a la Tierra, lo hizo a una velocidad de casi 1133 km/s y tuvo una extensión de 13.7x 10⁶fcm. Este evento produjo la disminución en la intensidad del campo magnético neto F de la Tierra por un intervalo de tiempo de 3 horas 21 minutos en el observatorio geomagnético de Villa Remedios. Por último, los resultados presentados son preliminares ya que falta ob­servar el registro del evento por el Detector de Neutrones Solares y así poder confirmar o rechazar alguna correlación con los datos del Monitor de Neutrones.

REFERENCIAS

1.- Space Environment Center-N.O.A.A. 2010, http ://www. sec .noaa.gov/today.html .xrav.        [ Links ]

2.- Rastogi, R. G. et al. 1999, PhysEarth PlamísSpace, 51, 947.        [ Links ]

3.-  Ricaldi, E. 2007, Observación simultánea de neutrones solares en asociación con una fulguración solar del 7 de septiembre de 2005 (HF-UMSA).        [ Links ]

4.-Ticona, R 2004, El Monitor de Neutrones (IIF-UMSA).        [ Links ]

5.- Watanabe, K. 2005, Solar Neutrón Events Associated with Solar Fiares (PhD Thesis).        [ Links ]

6.-  Zirin, H. 1965, Solar Fiares: Observations, Chapter 6 of Stellar and Solar Magnetic Fields (IAU Symposium No 22)        [ Links ]^rND^sRastogi^nR. G.^rND^nPedro^sMiranda Loza^rND^nFabricio G.^sÁvila Elías^rND^nPedro^sMiranda Loza^rND^nFabricio G.^sÁvila Elías^rND^nPedro^sMiranda Loza^rND^nFabricio G^sÁvila Elías

DISEÑO DE UN OSCILOSCOPIO MULTICANAL CON FPGA (PROYECTO LAGO)

 

THE DESIGN AND CONSTRUCTION OF A FPGA MULTI CHANNEL OSCILOSCOPE (LAGO PROJECT)

Pedro Miranda Loza¹ & Fabricio G. Ávila Elías²

¹ Instituto de Investigaciones Físicas-UMSA

² Carrera de Electrónica, Facultad de Ingeniería-UMSA

---

RESUMEN

Se diseñaron dos instrumentos basados en FPGA (Field Programmable Gate Array) para el proyecto LAGO (Large Aperture GRB Observatory) que facilitan la observación de señales eléctricas producidas por variaciones de rayos gamma de alta energía. Estos instrumentos son: osciloscopio de almacenamiento digital básico de alta velocidad con el que se puede observar las variaciones de las señales eléctricas en el tiempo, analizador multicanal que aporta datos cuantitativos acerca de la frecuencia con que las señales eléctricas alcanzan determinados niveles de voltaje. Ambos instrumentos se implementaron en hardware digital (re)programable de alta velocidad, utilizando Lenguaje de Descripción de Hardware (HDL). El despliegue y almacenamiento de los datos se realiza por un ordenador que facilita el acceso a funciones de control de los instrumentos. Para esto se desarrolló un software propio en visual C++. Se ha verificado el funcionamiento del diseño final conectado a un detector real en el Laboratorio de Física Cósmica en el monte Chacaltaya.

Descriptores: sistemas computacionales — instrumentos para rayos gamma

ABSTRACT

Two instruments based on FPGA (Field Programmable Gate Array) were designed and constructed for the LAGO (Large Aperture GRB Observatory) project. The instruments allow the observation of electric signáis producedby variations in high energy gamma rays. The instruments developed were: a high velocity basic digital storage oscilloscope which enables the observation of variations in electrical signáis over time, a multi channel analyzer that supports quantative data and picks up on the frequency at which electrical signáis reach certain voltages. Both instruments opérate with Language Description Hardware, a high velocity digital and reprogrammable hardware. The collection and storage of data is performed using a computer that facilítates access to the instruments' control functions. For this purpose original software was developed in C++. The design and function of the instruments were tested by connecting them to a real detector at the Cosmic Physics Laboratory at Chacaltaya, Bolivia.

Subjectheadings: computer systems — gamma ray instruments

---

1. INTRODUCCIÓN

En los experimentos de ñsica de partículas, las herramien­tas de adquisición y tratamiento de datos están en constante evolución. Son varios los factores que favorecen ésto, desde el aumento de la frecuencia de trabajo de los conversores análogo-digitales hasta la disponibilidad de realizar proto­tipos basados en FPGA (Field Programmable Gate Array), haciendo posible realizar un circuito integrado a medida, sin los riesgos económicos asociados a las otras opciones tec­nológicas. Aunque existen módulos especializados, disponi­bles comercialmente, éstos son de un costo mucho mayor al desarrollo de sistemas específicos.

El diseño de instrumentos de nueva generación con FPGA, está destinado a su utilización en el proyecto LAGO (Large Aperture GRB Observatory)¹, el cual está implementado para la observación de las variaciones de rayos gamma, Gamma Ray Burst (GRB), de alta energía. (Laboratorio de Física Cósmica-Chacaltaya)².

Las señales analógicas producidas por los detectores de ra­yos cósmicos de alta energía, tienen características especiales tales como: la duración del pulso, el valor máximo de éste, el tiempo promedio entre pulsos; siendo posible estudiar éstas señales mediante un Osciloscopio de alta velocidad. También es de interés el número de pulsos que se han producido en un

¹ Proyecto LAGO,

http://partículas.enea.gov.ar/experiments/lago.

² Proyecto LAGO-Bolivia,

http://www.f iumsa.edu.bo/iif/lago/inf ormes.

Pedro Miranda Loza & Fabricio G. Ávila Elías

Fig. 1.— Diagrama general de conexiones.

Fig. 2.— Diagrama funcional del diseño general.

 

intervalo de tiempo; esta tarea es realizada por un Analizador Multicanal, el cual tiene el propósito de contar dichos pulsos, además de clasificarlos por amplitudes.

Los detectores de Rayos Cósmicos (RC) del proyecto LAGO entregan una señal eléctrica de corta duración y am­plitud proporcional a la energía de la partícula. Para este efecto el detector está formado por las siguientes partes: Detector Cherenkov con agua (Water Cherenkov Detector-WCD), fotomultiplicador (PMT) y alimentación de alto vol­taje (HV).

Una de las principales características de la tecnología FPGA es la (re)programación del hardware digital por el usuario. Por lo que luego es posible diseñar nuevos ins­trumentos con una inversión mínima. Esto permite que un solo circuito digital en PCB (Tarjeta de Circuito Impreso) pueda desempeñar diferentes funciones según lo requiera la ocasión. Por ejemplo, en la implementación de los instru­mentos descritos más arriba, podría programarse el hardware como sólo Osciloscopio, o como Osciloscopio y Analizador Multicanal.

La velocidad en la captación y el proceso de datos, hacen del FPGA un dispositivo ideal para el experimento realizado; en vez de realizar la codificación de algoritmos en un microprocesador, éstos se mapean directamente en hardware. Esta última característica permite ejecutar instrucciones en para­lelo; logrando así que dos instrumentos, Osciloscopio y Ana­lizador Multicanal, procesen datos al mismo tiempo.

El costo económico estimado en la implementación del prototipo, comparado con el costo de una solución comer­cial es cinco veces menor. Por ello el Instituto de Investi­gaciones Físicas de la U.M.S.A. creyó que este proyecto se justificaría por su menor costo y aporte a la investigación en física cósmica.

Se elaboraron las GUFs (Graphic User Interface) en el or­denador para la visualización de las señales detectadas por los instrumentos. Además de proveer las funciones gráficas, el ordenador provee la mayoría de las funciones de control.

2. HARDWARE

En la Fig. 1 se muestra el diagrama general de conexiones entre el Detector, el Inversor de Alta Velocidad, el Disposi­tivo de Adquisición de Datos y el PC. El Inversor de Alta Velocidad es utilizado para invertir el pulso negativo gene­rado por el Detector, está construido con elementos discretos y tiene un ancho de banda de 300MHz con una impedancia de entrada de 1MCX

La señal (negativa) proveniente del Detector (fotomultipli­cador), es conducida a través de cable coaxial hasta el In­versor de Alta Velocidad, luego la señal (positiva) de salida del inversor es introducida al Dispositivo de Adquisición de Datos, éste digitaliza las señales analógicas y transmite los datos al PC, a través de una interfaz serial RS-232 con co­nectares DB9. Para la interfaz serial, es utilizado un cable de nueve hilos no cruzado (tipo módem).

El Dispositivo de Adquisición de Datos está conformado por una tarjeta de digitalización que contiene un conver-sor análogo-digital de 100MSPS (ADC08100-NationalIns­truments), y una tarjeta de desarrollo con el FPGA ACEX EP1K10TC100 (Altera).

Los bloques de la Fig. 1 a implementarse en el FPGA son: la memoria RAM donde se guardarán las muestras, la lógica de control y los módulos de recepción y transmisión de datos del puerto serial.

FlG. 3.— Ventanas de la interfaz gráfica.

3.  SOFTWARE

3.1. Diseño general

Tomando en cuenta la capacidad de los FPGAs de ejecutar instrucciones en paralelo, se han implementado el Oscilos-copio de Almacenamiento Digital y el Analizador Multica­nal en un mismo diseño escrito en lenguaje de descripción de hardware (HDL). Ya que los dos instrumentos ejecutan conjuntos de procesos por separado, y estos procesos ac­ceden a recursos compartidos, se ha visto de gran utilidad describir el diseño mediante diagramas de acceso, éstos son diagramas de interconexión funcionales para diseños concu­rrentes. En la Fig. 2 se tiene la representación funcional del diseño general, donde los componentes activos o procesos son presentados como círculos y los componentes pasivos como rectángulos, las flechas representan derechos de acceso o conexiones.

Los módulos OSC y PMCA corresponden a los dos ins­trumentos, Osciloscopio y Analizador Multicanal de Pulsos, respectivamente. Ambos módulos agrupan procesos y reali­zan el control de bancos de memoria RAM propios. También se puede observar que los procesos representados por dos círculos concéntricos son procesos que responden requeri­mientos de interrupción (IRQ), que deben entenderse desde el punto de vista del dispositivo: éste se encuentra realizando un proceso y a partir de un evento se pone en marcha otro proceso.

Ambos módulos utilizan recursos comunes, el mismo ca­nal de comunicación con el ordenador(puerto serial) para en­viar datos y recibir comandos, y los datos entregados por el conversor análogo digital; éste se encuentra configurado en modo libre, entregando el resultado de una conversión cada 10 ns.

El proceso FADC realiza un seguimiento continuo de la señal digital de entrada, una vez que esta señal cumple cier­tas condiciones, éste proceso avisa al módulo OSC que co­mience la grabación de los datos digitales en posiciones con­secutivas de la memoria RAM. Una vez que se han grabado todas las posiciones de la memoria disponibles, el módulo OSC accede al proceso Rx/Tx, y envía el contenido total de la memoria RAM al ordenador a través de la interfaz serial.

De manera similar ocurre el funcionamiento del módulo PMCA, el proceso FADC identifica el máximo (digital) de un pulso, con este dato accede al módulo PMCA, éste a su vez actualiza la cuenta del respectivo canal (en la memoria del espectro) y devuelve el control al proceso FADC. Si el módulo PMCA recibe el comando enviar todos los datos de la memoria de espectro al ordenador, se detiene el proceso de actualización del PMCA, se accede al proceso Rx/Tx y se envía el contenido total de la memoria de espectro al ordena­dor a través de la interfaz serial.

Las opciones implementadas para el instrumento Oscilos­copio son las siguientes: velocidad de muestreo, nivel de dis-

FlG. 4.— Curva de platean para PMT 9353KB.

paro, pendiente de disparo, predisparo y autodisparo. Las op­ciones implementadas para el instrumento Analizador Mul-ticanal son: nivel de discriminación o umbral, control de inicio/fin, borrado de toda la memoria de espectro, envió de datos al ordenador.

3.2. ínter faz gráfica

El software escrito en visual C++ realiza las siguientes fun­ciones:

—Acceso al puerto de comunicación serial del ordenador para adquirir los datos.

—Proceso y despliegue gráfico de los datos capturados por el instrumento.

—Operación de las funciones del instrumento a través de una interfaz gráfica de usuario.

El acceso al puerto serial se realizó a través de funciones de API de Windows, que facilitó el manejo de buffers de datos de envío y recepción y la modificación de los parámetros de transmisión. Teniendo en cuenta la gran utilidad de visuali­zar los datos capturados por el instrumento, el despliegue de gráficos se realizó utilizando librerías OpenGL³, que facilitan la representación de datos y su animación en dos dimensio­nes, logrando de esta manera una representación adecuada para los instrumentos Osciloscopio y Analizador Multicanal.

Un ejemplo del despliegue de datos en la interfaz gráfica se puede observar en la Fig. 3. En la parte superior está la ventana correspondiente al instrumento Osciloscopio con un pulso generado por el detector de Rayos Cósmicos, en la parte inferior está la ventana del Analizador Multicanal de pulsos con un espectro característico de Rayos Cósmicos y en la parte derecha está el menú de opciones de los instru­mentos.

4.   RESULTADOS

Una vez efectuadas varias pruebas con un generador de funciones, se verificó que la interfaz gráfica en la PC mues­tra correctamente los datos captados por el instrumento Osci­loscopio. Los controles proveídos en el diseño hacen posible que se puedan observar señales en el rango de frecuencias de IKHz hasta 50MHz; el límite superior es dado por el

³ OpeGL UserInterfaceLibrary, http://glui.sourceforge.net.

teorema de Nyquist ya que el ADC utilizado trabaja a una frecuencia de 100MHz. Aunque en la práctica, para obtener una forma de onda más detallada es necesario tener por lo menos nueve muestras, en vez de dos muestras por periodo. Esto hace que la máxima frecuencia, presente en la señal a analizar debe ser de jq la frecuencia de muestreo. Los pulsos producidos por un PMT tienen una frecuencia aproximada de 40MHz, estos pulsos son detectados por el instrumento Osciloscopio (dos o tres muestras por pulso) y registrados en un archivo para posterior análisis.

Se aplicó el instrumento Analizador Multicanal de pulsos a la determinación de la curva de platean para un fotomulti-plicador9353KB deElectron Tubes⁴. Elfotomultiplicadorse encuentra instalado conjuntamente a un centelleador de agua, denominado WCD3, en el Laboratorio de Física Cósmica, en el monte Chacaltaya.

Se polarizó con alto voltaje (HV) el fotomultiplicadory se realizó el conteo de pulsos durante un tiempo fijo. Se polarizó el PMT de 900 a 1700 V, en intervalos de 100 V.

Los resultados de la aplicación se observan en la Fig. 4 en escala lineal y logarítmica. En esta ultima se puede apre­ciar mejor la región en la que un aumento del alto voltaje causa una menor diferencia entre las cuentas. Entre 1100 V y 1400 V está un segmento con menor pendiente; por lo tanto en ese segmento, a diferencia de otros, las cuentas no au­mentarán significativamente conforme vaya aumentando el alto voltaje. Según la Fig. 4, el valor sugerido para polari­zar el PMT es de 1200 V, y éste es el valor⁵ elegido para la operación de WCD3 en Chacaltaya.

Además de las cuentas totales de pulsos, también se dis­pone del espectro de picos, correspondiente a cada alto vol­taje aplicado al PMT de WCD3. Se han comparado estos es­pectros con las mediciones independientes realizadas por el proyecto LAGO para WCD3, y se ha verificado que los es­pectros son similares para cada alto voltaje.

Los instrumentos descritos han sido diseñados para su uso específico en la observación de señales eléctricas rápidas, producidas por rayos cósmicos, en general de alta energía,

⁴ Electrón Tubes Enterprises Ltd., //www. electrontubes. com.

⁵ Este valor fue elegido después de varias pruebas con equipos especiali­
zados instalados en Chacaltaya.

del proyecto LAGO, pero éstos también tienen un uso gene­ral. En el caso del Osciloscopio, puede utilizarse como un instrumento de laboratorio de nivel universitario, para la ob­servación de señales periódicas y no periódicas, dada su alta tasa de conversión (100 MSPS). En el caso del Analizador Multicanal, éste es muy útil en análisis de espectroscopia nuclear, en el cual la distribución de probabilidad de la ra­diación detectada está en función de su energía. El Analiza­dor Multicanal también puede utilizarse en aplicaciones en las que se requiera el conteo de pulsos.

REFERENCIAS

1.- Rivera, B. H. 2007, Implementación y Calibración de un Prototipo de Detec­tor Cherenkov de Chubascos Atmosféricos (Tesis de Grado, Universidad Mayor de San Andrés)        [ Links ]^rND^sRivera^nB. H.^rND^sJosé Antonio^nZelaya^rND^sJosé Antonio^nZelaya^rND^sJosé Antonio^nZelaya

DOS PASIONES: LA FÍSICA CÓSMICA Y LAS NIEVES ANDINAS

 

TWO PASSIONS: COSMIC PHYSICS AND ANDEAN SNOWY PEAKS

 

Gral. Ing. José Antonio Zelaya Academia Nacional de Ciencias de Bolivia

---

RESUMEN

De la historia del Laboratorio de Física Cósmica de Chacaltaya. El Ing. José Antonio Zelaya rememora su experiencia como investigador en el laboratorio en la época inicial cuando el Dr. Ismael Escobar, fundador del Laboratorio, era su Director.

Descriptores: historia de la ciencia — observatorios — rayos cósmicos

ABSTRACT

A history of the Cosmic Physics Laboratory at Chacaltaya. José Antonio Zelaya reminisces about his experiences as a researcher at the Laboratory during its beginnings when Dr. Ismael Escobar, founder of the Laboratory, was Director.

Subjectheadings: history of science — observatories — cosmic rays

---

"La vida atrae la vida, nada ocurre por azar" Javier Sierra.

La atracción de las nieves andinas y por el esquí, inspi­raron al Profesor universitario Dr. Ismael Escobar, para pro­mover las investigaciones de Física Cósmica en el nevado de Chacaltaya. Su entusiasmo consiguió despertar el interés del rectorado de la UMSA, y también el interés de otras univer­sidades del exterior. Su plan inicial fue instalar una estación meteorológica y poco a poco las instalaciones. A partir de las primeras habitaciones fueron agregándose otras para re­cibir las expediciones extranjeras que solicitaban llegar a este laboratorio que poco a poco fue adquiriendo fama internacio­nal.

Cuando en 1964, el Ing. Ramón Schulczewski ini­ciaba otro experimento internacional sobre estudios de la ionosfera, llegó la primera antena parabólica a Bolivia, fui invitado para orientar astronómicamente mediante un azimut geodésico. En dos noches, utilizando la estrella polar del Sur, la Sigma Octantis, logramos cumplir con el pedido. Nos pi­dieron la cuenta por el trabajo realizado y mi respuesta fue que se trataba de una colaboración a la UMSA, donde ya dictaba la cátedra de astronomía geodésica. Cuando pasaron algunos años recibí un llamado telefónico para visitar al Di­rector del "Laboratorio de Física Cósmica" Dr. Escobar. En muy breves palabras me invitó para integrar la planta de in­vestigadores del Laboratorio. Por mi grado militar de Mayor, le dije que tendría que solicitarse siguiendo el conducto re­gular mediante una nota al Comandante del Ejército. Así lo hizo y a la semana me volvió a llamar y me dio la nota de res­puesta del Comando del Ejército, negando mi participación. Recuerdo sus palabras: "No entiendo, cómo una institución como el Ejército se niega conseguir el prestigio de participar en la investigación científica en el ya famoso Laboratorio de Física Cósmica de Chacaltaya, otra institución militar se sentiría halagada por esta invitación - Deje que yo aplique mis métodos." Yo levanté los hombros, dando así mi con­sentimiento para que ponga en práctica su idea. Llamó a su secretaria y pidió hablar con el Dr. Paz Estenssoro, Presi­dente de la República, a los pocos minutos escuché la con­versación y me dijo "esperaremos la respuesta", unos minu­tos más y evidentemente recibió la respuesta. Y, volviéndose me dijo, "bienvenido Mayor como Investigador asociado, en comisión del Ejército cumpliendo las leyes de oficiales en co­misión." Esta anécdota, explica la capacidad emprendedora del Dr. Escobar. Cuando llegué por primera vez a Chacaltaya se me asignó una habitación en el segundo piso donde ya estaban instalados varios equipos de investigación; dormí en el piso porque no habían catres. Al comedor llegábamos en tres turnos, donde se reunían americanos, japoneses e inves­tigadores bolivianos. Durante un año realicé en el nevado, a 5.420 metros de altura, las investigaciones sobre las "Nubes de libración en las constelaciones opuestas a la trayectoria de la Luna para evitar interferencias en las placas de emulsión en la cámara con telescopio incluido. El Dr. Stevenson, del Servicio Geológico de los Estados Unidos, me dio las ins­trucciones para las operaciones en la obtención de las pla­cas con exposiciones hasta de 10 minutos escogiendo una estrella de seguimiento, en los mapas estelares en los lugares aproximados a los puntos de libración de la Luna. En dos no­ches de trabajo obtuvimos 8 placas, las que procesamos en la cámara oscura del laboratorio. Satisfecho con mi trabajo, el Dr Stevenson, me dejó que realizara solo todo el proceso, sin importarme la fatigosa ascensión al nevado, ni el frío (23° bajo cero) y los fuertes vientos que había que soportar. La cúpula plateada que adornaba la cumbre de la pista de esquí, presentó un inconveniente, reflejaba el brillo de algunas es­trellas en la sensible emulsión cuando el obturador estaba abierto. Recibí una carta para que detectara el inconveniente y, al comprobar que se trataba de la cúpula, avisé al Dr. Es­cobar y cuando me preguntó la solución le dije que había que construir otro mojón de soporte para la cámara a la intempe­rie algo alejada de la cúpula. Muy rápidamente se realizó el traslado y las placas obtenidas ya no presentaban interferen­cias, pero la falta de protección aumentaba la incomodidad del frío y el viento. Cuando la motivación del trabajo llegó a despertar mi curiosidad personal, aumenté las exposiciones hasta 20 minutos y luego hasta 30 minutos. Las placas así obtenidas me mostraron la inmensidad del misterioso cos­mos. El motivo principal de la investigación era descubrir las rocas en suspensión o equilibrio gravitacional llamadas las rocas de Kordalewsky —un astrónomo polaco que escribió su teoría de las nubes de libración en las que se encontraban rocas de hasta 200m de longitud—, provenientes de las co­lisiones de meteoros o meteoritos en la superficie lunar, las mismas que dejaron las huellas como cráteres volcánicos. La teoría agregaba que de las altas montañas estas rocas incluso se las podría ver a simple vista. Cuando cumplí la fecha de mi compromiso fui preguntado por carta si había visto las rocas a simple vista, mi respuesta fue clara, siguiendo el dictado que me enseñaron en la EMI. La ciencia es la búsqueda de la verdad. Y dije, "no, no he visto". Al poco tiempo el hom­bre llegó a la Luna. Recibí una nota de agradecimiento por mi trabajo, indicándome que en una reunión de científicos en el Servicio Geológico, había ocupado el segundo lugar entre los trabajos científicos más sacrificados que se hacían en el mundo, el primer lugar lo ocupó un investigador de los pe­ces ciegos en Laponia donde se cavaron pozos en el hielo y los investigadores zambullían para agarrar los peces con las manos y subirlos a superficie.

Durante mi estadía en Chacaltaya logré la donación de 20 catres del Ministerio de Defensa, fui nuevamente invitado para colaborar en la investigación del ozono en superficie, en el manejo de los telescopios para la detección de mesones pesados en interior mina y en el procesamiento de datos me­teorológicos y paralelamente, mientras trabajaba en las no­ches, durante el día colaboré como guía para atender la gran cantidad de turistas que visitaban las instalaciones incomo­dando muchas veces la atención de los investigadores. El Dr. Escobar agradeció mis servicios y se despidió cuando fue distinguido para ocupar un cargo en el exterior. Guardo para él los más gratos recuerdos del mismo modo para los colegas extranjeros y bolivianos con los que tuve la oportunidad de iniciar una permanente amistad.

Los trabajos realizados en Chacaltaya fueron tomados en cuenta para ocupar la silla de Astronomía en la Academia de Ciencias, que había dejado vacante el padre De Cotte del observatorio del Colegio San Calixto. Con el tiempo, ocupé la dirección del Instituto de Investigaciones Físicas de la UMSA y logré que la sección de Construcciones de la Uni­versidad aprobara los planos arquitectónicos para un nuevo laboratorio en Chacaltaya. Estos planos deben estar en los archivos correspondientes.

XXI REUNIÓN NACIONAL DE LA SOCIEDAD BOLIVIANA DE FÍSICA

DEL 26 AL 31 DE OCTUBRE DE 2009

COCHABAMBA-BOLIVIA

 

Sociedad Boliviana de Física

---

RESUMEN

Se presenta la relación de ponencias de la XXI Reunión Nacional de Física realizada en Cochabamba entre el 26 y el 31 de Octubre de 2009.

Subject headings: physics workshops

---

Título:

EVALUACIÓN DEL MODELO CLIMÁTICO REGIONAL PRECIS PARA EL ÁREA DE BO-LIVIA: COMPARACIÓN CON ESTACIONES DE SUPERFICIE

Autor:

Marcos Froilán Andrade Flores

Resumen:

Los posibles efectos del cambio climático sobre re­giones como Bolivia son de mucho interés tanto a ni­vel científico como político. Una de las herramientas más importantes para estudiar estos efectos son los modelos numéricos del clima. A fin de establecer la confiabilidad de las proyecciones de la evolución del clima futuro producidas por dichos modelos es nece­sario, sin embargo, validar las salidas de los mismos. En este trabajo se estudia el comportamiento del mo­delo climático regional PRECIS (Providing REgional Climates for Impacts Studies) del Hadley Centre de la Oficina Meteorológica Inglesa, sobre la región de Boli-via. La comparación de resultados del modelo con da­tos observados en superficie a nivel mensual de tempe­ratura y precipitación en el periodo 1961-1990 mues­tran que el modelo tiene un buen desempeño en zo­nas bajas (menos de 500 m snm) pero que sobreestima precipitación tanto en zonas de altura intermedia (entre 500 y 3500 m snm) como en la zona andina (situada a una altura mayor a 3500 m snm). A su vez la compa­ración muestra que el modelo subestima la temperatura (media, máxima y mínima) en la mismas dos regiones mientras que realiza un trabajo aceptable en las zonas bajas. Aunque la parametrización de nubes y precipi­tación en las zonas de los valles y andina parece ser el elemento que más podría contribuir a las diferencias observadas es necesario un estudio más profundo para entender los mecanismos involucrados.

Título:

HERRAMIENTAS TECNOLÓGICAS Y EL PRO­CESO DE ENSEÑANZA APRENDIZAJE EN AULA PARA LA MATERIA DE FÍSICA

Autor:

Milka Mónica Torrico Troche

Resumen:

La Física como ciencia es indispensable en la for­mación de los futuros profesionales de Ciencias e In­genierías, considerando como población los estudian­tes que cursan los primeros semestres de las carre­ras de Ciencias e Ingenierías de las Universidades pu­blica y privadas de la provincia Cercado del Departa­mento de Cochabamba, las estadísticas nos muestran muchas deficiencias en la respuesta de los estudian­tes hacia la materia de Física Básica, promoviendo un análisis de la situación que se centra en el proceso de enseñanza en aula, identificando a través de encues­tas a docentes y estudiantes involucrados en el pro­ceso, tres problemas, que son: (i) deficiencia de mate­rial bibliográfico adecuado; (ii) falta de visualización del fenómeno físico en los estudiantes; (iii) deficien­cia en la comunicación docente - estudiante. De esta manera el presente trabajo tiene por objetivo: diseñar una guía metodológica que involucren el uso de nue­vas herramientas tecnológicas, para mejorar el proceso de enseñanza aprendizaje en aula en la asignatura de Física Básica de las carreras de Ciencias e Ingenierías, tomando en cuenta los diferentes métodos didáctico y recursos didácticos, donde se incorpora el uso de he­rramientas computacionales en función a su aplicabi-lidad con el campo de la Física. Una vez definidos los métodos y recursos se planifica el desarrollo de las cla­ses, estructurando las actividades, material, contenido, herramientas y recursos en un PLAN DE CLASES, que se constituye en una guía para el docente. El Plan de Clases lo elabora cada docente definiendo el rumbo que tomara la clase, de esta manera la introducción de las nuevas herramientas tecnológicas promueve interés en el estudiante que esta habituado a la nueva tecno­logía y la gama de alternativas computacionales per­mite que el docente se convierta en investigador en el proceso de enseñanza, recuérdese que enseñar es un arte donde el artista es el docente. Finalmente se muestra como ejemplo parte de la aplicación de la guía metodológica propuesta a la materia de Física II, tema Estática de Fluidos. generales y sobre la que no existe aún un concepto uni­versal o una ciencia unificadora que valga para todos los ámbitos donde ella aparece. En el presente trabajo, el autor concibe una base teórica firme sobre la cual construye una teoría que explica el fenómeno de la complejidad de una manera coherente como un plan­teamiento científico inédito.

Título:

MAPA DE RADIACIÓN SOLAR PARA SOLIVIA

Autor:

Marcelo Javier Lucano

Resumen:

En este trabajo se estimaron los valores de la radiación solar global a través de modelos de Sistemas de In­formación Geográfica e imágenes satelitales obtenidos a través de la metodología SSE de la NASA para un periodo de registros de 22 años. Con estos valores de radiación, se obtuvo la distribución temporal y espa­cial de la radiación solar para Bolivia mediante un pro­ceso de interpolación utilizando el paquete de análisis geoestadístico ILWIS, considerando datos de 182 gri­llas de I^o x I^o que abarcan la zona de estudio y uti­lizando el método de superficie móvil con distancia inversa, exponente de peso 2, distancia esférica y se­gundo grado parabólico. Se observó que los niveles de radiación más bajos corresponden a los meses de mayo a julio que pertenecen a la estación de invierno y los niveles de radiación más altos corresponden a los meses de octubre a diciembre que pertenecen a las es­taciones de primavera y verano. Asimismo, se observó que la parte noreste de Bolivia, a partir de la Cordi­llera Oriental presenta los valores más bajos de media anual de radiación global, entre 3.9 - 5.1 kW-h/m²-día, en tanto que, en la zona suroeste la radiación solar aumenta con valores entre 5.1 - 7.2 kW-h/m ²-día.

Título:

LA TEORÍA DE LA ORGANIZATIVIDAD: 'EL FINAL DE LA TERMODINÁMICA CLÁSICA Y EL COMIENZO DE LA ORGANIZATIVIDAD' (UNA TEORÍA QUE EXPLICA LA COMPLEJI­DAD)

Autor:

Andrés Trepp del Carpió

Resumen:

La complejidad es una cualidad abstracta de ciertos sistemas de la naturaleza y del mundo humano cul­tural, de la que hoy sólo se conoce sus características

Título:

BÚSQUEDA DE ANTIMATERIA EN EL UNI­VERSO

Autor:

Kenny Choque Talavera

Resumen:

El modelo estándar de la física de partículas establece que tanto partículas como antipartículas fueron crea­das simultáneamente en cantidades iguales. Según el modelo estándar del Big Bang, el Universo fue creado en un tiempo primordial. Es natural pensar que en el inicio del Universo, materia y antimateria fueron crea­das en cantidades iguales. Sin embargo, las observa­ciones astronómicas muestran que el Universo obser­vable está constituido por materia. La aparente asi­metría entre materia y antimateria es un enigma fun­damental de la ñsica de partículas y también de la as­tronomía. Si la antimateria existe en algún lugar del Universo, la búsqueda de señales de rayos gamma pro­venientes de su aniquilación, o aun, de rayos cósmicos de antipartículas, serían indicadores de la existencia de dominios de antimateria.

Título:

¿ES LA HORCA DEL INCA UN OBSERVATO­RIO ASTRONÓMICO?

Autor:

Gonzalo Pereira Quiroga

Resumen:

A propósito de la conmemoración del Año Internacio­nal de la Astronomía, algunos estamentos medios del Gobierno de Bolivia, se han enfrascado en tramitar la declaratoria de "Patrimonio Astronómico de la Huma­nidad" ante la UNESCO, al monumento arqueológico de la Horca del Inca, situado en la localidad de Copa-cabana. Uno de sus principales argumentos para obte­ner la declaratoria de patrimonio astronómico es una serie de trabajos arqueoastronómicos y de datación atribuidos al Laboratorio de Física Cósmica de la Uni­versidad Mayor de San Andrés. La ponencia que pro­ponemos presentar es el resultado de un análisis de los trabajos, tanto arqueológicos como astronómicos, que se emplean para apoyar la propuesta: La Horca del Inca es un Observatorio Astronómico.

Título:

PRUEBAS DE ALINEALTDAD POR DATOS SU­BROGADOS

Autor:

Y Miguel Peñafiel N.

Resumen:

Se analiza un registro de las tres componentes del campogeomagnético (Patacamaya) mediante datos su­brogados de Fourier y subrogados restringidos para de­cidir sobre sus características de linealidad. Se com­para los resultados obtenidos con los correspondientes coeficientes maximales de Liapunov.

Título:

MÉTODO DE DEPROYECCIÓN Y OBTENCIÓN DE LA ESTRUCTURA DE BRAZOS DE GALA­XIAS ESPIRALES

Autor:

Deterlino Urzagasti

Resumen:

Se desarrolla un método para la deproyección de imágenes de discos de galaxias espirales sin barra y la obtención de su estructura de brazos mediante el mo­delo de espirales logarítmicas. El método se basa en la obtención de los puntos de máximos y mínimos locales de las fluctuaciones de la intensidad en las imágenes galácticas a través de un proceso de suavizado con el filtro de Savitzky-Golay. Estos puntos luego sirven para determinar los ángulos de inclinación y de po­sición del disco galáctico así como el pitch angle de sus brazos espirales. El método se aplicado a varias galaxias espirales, encontrándose un buen acuerdo con otros resultados de la literatura.

Título:

ANÁLISIS DE PATRONES EN FRACTALES

Autor:

Flavio Ghezzi

Resumen:

Se discute la dimensión frac tal de sistemas deter-minísticos y no-determinísticos haciendo énfasis en la relación entre la dimensión fractal y diferentes parámetros ñsicos. Finalmente, se discute la invarian-cia de escala de sistemas coloidales.

Título:

AUTOSIMILARLDADES EN EL ESPACIO DE PARÁMETROS PARA EL CmCUITO DE CHUA

Autores:

Marcelo Ramírez Ávila, Jason Gallas

Resumen:

Se muestran autosimilaridades en el espacio de parámetros del circuito de Chua, considerando tanto una función lineal por partes, así como una función cúbica. También se muestra el isomorfismo entre los planos de fase para ambas no-linealidades.

Título:

ASPECTOS TEÓRICOS DE LA TEORÍA ESPE CIAL DE LA RELATrVTDAD

Autor:

Luis Panfilo Yapu Quispe

Resumen:

Se describe la estructura del grupo de Lorentz que per­mite relacionar la teoría especial de la relatividad con otras áreas de la física moderna. Para ilustrar esta des­cripción se deducirán algunas fórmulas "clásicas".

Título:

OSCILACIONES DE BLOCH EN UN CIRCUITO CUÁNTICO INDUCTIVO ACOPLADO A LAS

VIBRACIONES DE UNA RED

Autor:

Marcelo Calcina Nogales

Resumen:

Se acopla un circuito puramente inductivo con carga discreta a los modos vibracionales de una red unidi­mensionales (fonones). Los modos vibracionales de­forman el anillo y por lo tanto se modifica su inductan-cia (sistema electromecánico-cuántico). Cuando este anillo se conecta a una fuerza electromotriz de valor £o, el periodo usual de la corriente (q_e £o/V) se ve afectado por un armónico con periodo igual al doble de su valor original (2q_e £o/V). Este fenómeno es equi­valente al de las oscilaciones de Bloch en un cristal en el cual el electrón experimenta una frecuencia de osci­lación aFIW. En nuestro caso, la carga eléctrica funda­mental q_e juega el rol de la constante de red.

Título:

LOS COMETAS METEOROLÓGICOS

Autores:

Grupo Astronáutico Boliviano

Resumen:

Se estudiaron dos tipos de cometas de papel (delta y rombo) y su desempeño bajos las condiciones at­mosféricas de La Paz, con el fin de diseñar cometas capaces de elevar un equipo de medición atmosférica. La gran preferencia de usar cometas en lugar de glo­bos aerostáticos se basa en la facilidad de recuperar los instrumentos de medición así como en la economía para construirlos. Comprobamos que el método de unir varios cometas es adecuado poder elevar una carga de prueba y alcanzar una altura mayor sin perder estabili­dad. Lo primero que se hace es elevar un cometa piloto que cuando está estable jala a un segundo cometa que lleva la carga de prueba, y así se siguen uniendo varios cometas hasta alcanzar alturas ideales de unos 250m.

Título:

PROYECTO "LAGO"

Autor:

Alfonso Ve larde Chave z

Resumen:

Se describe la instalación y puesta en marcha de la es­tación LAGO-Bolivia.

Título:

"SISTEMATIZANDO" LA INVESTIGACIÓN CIENTÍFICA

Autor:

Marco Antonio Córdova Olivares

Resumen:

Por mi experiencia a lo largo de mi formación académica, he visto "desvanecerse" trabajos de inves­tigación tanto de docentes como de estudiantes, ya que caen en "saco roto". Ello se debe a que no existe una política institucional ni gubernamental que pueda "agarrar" estos trabajos de investigación. En este sen­tido, propongo un método que facilita la digitalización y el control de todos los trabajos de investigación científica, tanto a nivel personal como institucional, enfocando mi propia experiencia sobre la construcción de mi trabajo de tesis.

Título:

DOSIMETRÍA DE NEUTRONES - MONITOR DE NEUTRONES

Autor:

Rolando Ticona Peralta

Título:

ESTUDIO DE LA SINCRONIZACIÓN DE PÉNDULOS ACOPLADOS MEDIANTE SIMU­LACIONES COMPUTACIONALES

Autores:

Armando Reynaldo Ticona Bustillos, Marcelo Gon­zalo Ramírez Ávila

Resumen:

Usando un modelo discreto de péndulo amortiguado, estudiamos las condiciones de sincronización para dos péndulos acoplados. En primer lugar analizamos las cuencas de atracción estudiando la razón entre los pe­riodos de los dos péndulos (Ti/T{) para diferentes con­diciones iniciales, es decir, diferentes ángulos desde los cuales los péndulos inician su movimiento, consi­derando para ésto diferentes relaciones de largo, masa, acoplamiento entre péndulos y disipación. A partir de estos resultados podemos caracterizar las lenguas de Arnold, analizando nuevamente el comportamiento de la relación entre periodos en función a las condicio­nes iniciales de uno de los péndulos y los diferentes valores de masa, largo, acoplamiento y disipación. En estos gráficos podemos identificar sincronización 1 : 1 así como sincronizaciones de otros órdenes (m : n) y también regiones cuasi periódicas, las cuales podrían conducirnos también a regiones caóticas en trabajos futuros; además se tienen todas las condiciones para ampliar este trabajo a más de dos péndulos.

Título:

CAMAS SOLARES

Autores:

Emiliana Juaniquina, Fernando Ve larde, Flavio Ghezzi, Armando Ticona

Resumen:

Se realiza la caracterización del espectro de emisión electromagnética de una lámpara fluorescente usada en camas solares, para esto usamos un espectro fotómetro, que nos permite analizar el espectro desde aproximadamente 180nm, hasta aproximada­mente 880nm, dividiendo este intervalo en 3500 ca­nales. Debido a que el espectro fotómetro adquiere los datos mediante una fibra óptica, las limitaciones de ésta no nos permiten analizar todo el espectro, dejándonos sólo información entre las bandas UVB y el visible. Las lámparas usadas en estas camas solares deberían tener una emisión rica en la banda del UVA, lo que permitiría el bronceado; y el resto de emisión debería estar en el visible. Nuestros resultados mues­tran un contenido pequeño de UVB en la emisión de dichas lámparas, lo cual representa un peligro debido a lo nocivo de este tipo de radiación, por lo cual se recomienda un uso muy cuidadoso y supervisado de dichos instrumentos cosmetológicos.

^rND^nA. R.^sTlCONA BUSTILLOS^rND^nG. M.^sRAMÍREZ ÁVILA^rND^nA. R.^sTlCONA BUSTILLOS^rND^nG. M.^sRAMÍREZ ÁVILA^rND^nA. R^sTlCONA BUSTILLOS^rND^nG. M^sRAMÍREZ ÁVILA

DETERMINACIÓN DEL COEFICIENTE DE DISIPACIÓN DE UN PÉNDULO

 

DETERMINATION OF A PENDULUM'S DISSIPATION COEFFICIENT

 

A. R. TlCONA BUSTILLOS & G. M. RAMÍREZ ÁVILA

Instituto de Investigaciones Físics

Universidad Mayor de San Andrés La Paz - Bolivia

---

RESUMEN

Usando un sensor de posición se toman datos de las oscilaciones de un péndulo amortiguado. Analizando las características del péndulo se determina su coeficiente de disipación.

Descriptores: procedimientos de laboratorio — dinámica de la partícula

ABSTRACT

Using a position gauge we register data from the oscillations of a damped pendulum. We analize the pendulums characteristics and determine its dissipation coefficient.

Subjectheadings: laboratory procedures — dynamics of the particle

---

El movimiento armónico simple (MAS) encuentra aplicaciones en muchas ramas de la física; sin embargo, la primera dificultad con la que se tropieza al comparar sus resultados con oscilaciones reales, es la disipación de energía mecánica debida a la interacción de estos sistemas con el medio viscoso que los rodea. Esto hace que los sistemas reales sólo obedezcan por un tiempo relativamente corto los resultados de las soluciones del MAS. El problema de introducir el término de disipación (que puede ser función de la velocidad, de la masa y forma del objeto, así como de la viscosidad del medio) en las ecuaciones está en que éstas ya no son sencillas pues pierden su carácter lineal y por tanto, la solución de las mismas no es inmediata y se deben recurrir a aproximaciones o directamente a la resolución numérica de las ecuaciones. En este trabajo, se presenta un ejemplo de cómo medir directamente este coeficiente mediante las oscilaciones de un péndulo cuya lenteja puede ser considerada como un objeto puntual, utilizando un sensor de movimiento que nos da la posici´on de la lenteja del péndulo en función del tiempo. Este trabajo surge como parte de la investigación realizada en el estudio de péndulos acoplados (Ticona Bustillos & Ramirez Avila 2008).

2. PÉNDULO CON DISIPACIÓN

Se considera un péndulo con masa puntual, como se muestra en la Fig. 1. Las fuerzas que actúan sobre este objeto son el peso y la fuerza de disipación por parte del aire. Aplicando la segunda ley de Newton en la dirección del movimiento, se tiene:Pero la aceleración se puede expresar en función del desplazamiento angular como:

Además, considerando desplazamientos angulares pequeños para los cuales se cumple senf9 « 9, la ecuación se reduce a:

que tiene una solución conocida y detallada en libros de física general (Halliday & Krane 1998; Serway 1997; Tipler 1995) dada por:

angular dadapor:

 

 

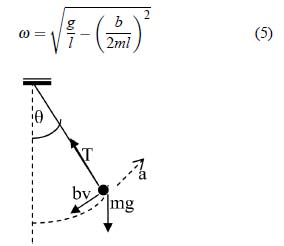
FIG. 1.— Diagrama de fuerzas y aceleración para el péndulo con disipación.

 

FIG. 4.— Ángulo del péndulo en función del tiempo.

La frecuencia angular es menor a la del péndulo sin amortiguamiento, debido a la interacción con el medio viscoso.

3. MEDIDA DEL COEFICIENTE DE DISIPACIÓN

Utilizamos un sensor de posición PASCO, el cual toma datos de la distancia de un objeto a partir de un nivel de referencia, como se muestra en la Fig. 2. Estos datos son enviados a una computadora. Se utilizó un péndulo de 53.0cm de largo y 150.Og de masa. La aceleración debida a la gravedad en la ciudad de La Paz se considera igual a 9.775m/s². Los datos obtenidos se muestran en la Fig. 3. En estos datos, se puede observar que las distancias muy cercanas al detector no son obtenidas correctamente debido a la propia sensibilidad del detector; además, existen algunos casos en los que el péndulo no es detectado cuando está en la máxima distancia, dándonos el dato de la pared que está a mayor distancia.

Como se conoce el largo del péndulo, se pueden transformar estos datos a ángulos con lo que se obtiene el gráfico de la Fig. 4, donde sólo se consideran los datos a partir del movimiento del péndulo; en estos datos también se realizó un desplazamiento desde el nivel de referencia mostrado en la Fig. 3.

En la ecuación (4) se pueden considerar solamente los máximos de las oscilaciones, es decir, los puntos en lo cuales el coseno es igual a la unidad. En ese caso sólo nos quedamos con la parte exponencial del comportamiento.

De igual manera, esto puede ser realizado con los datos obtenidos con el detector, tanto en las distancias mínimas como en las máximas. Como mencionamos antes, las distancias menores tienen un problema debido al detector, por lo cual sólo consideramos las distancias máximas en cada oscilación. De esta manera, se puede obtener el ajuste exponencial mostrado en la Fig. 5.

Para obtener la Fig. 5, algunos de los puntos han sido eliminados, ya que quedaban fuera de la línea de ajuste, debido a las circunstancias ya explicadas. A partir de este ajuste podemos determinar que el valor del coeficiente de disipación es igual a 0,013 kg/s.

4. CONCLUSIONES

Este método nos brinda una forma muy sencilla de calcular el coeficiente de disipación de un objeto

relativamente pequeño, sin tomar en cuenta medidas de los factores geométricos ni la viscosidad del fluido.

FIG. 5.— Ajuste exponencial del ángulo en función del tiempo.

 

REFERENCIAS

1.-Halliday, R. & Krane. 1998, Física, vol. 1, cuarta ed. (CECSA).

        [ Links ]

2.- Serway, R. 1997, Física, vol. 1, cuarta ed. (McGraw-Hill).

        [ Links ]

3.- Ticona Bustillos, A. R. & Ramírez Avila, G. M. 2008, RBF, 14, 121.

        [ Links ]

4.-Tipler. 1995, Física (Reverte)

        [ Links ]^rND^sHalliday^nR.^rND^sTicona Bustillos^nA. R.^rND^sRamírez Avila^nG. M.^rND^sChoque Saire^nM. P.^rND^sChoque Saire^nM. P.^rND^sChoque Saire^nM. P

LA OCARINA DE ZANAHORIA A CARROT OCARINA

Choque Saire M. P.

Laboratorio de Física 121 Universidad Mayor de San Andrés

---

RESUMEN

En los instrumentos prehispánicos aerófonos el sonido es producido por la vibración de una columna de aire como es el caso de la quena, la zampona y la tarkha. Se suele olvidar, sin embargo, a otros instru­mentos pertenecientes a esta misma familia, como es el caso de la ocarina, cuya afinación y fabricación es dificultosa. Este instrumento musical es de tamaño reducido, su sonido es agudo (523 - 1046 kHz) y se la encuentra en múltiples diseños. Su construcción es ardua debido a que habitualmente las ocarinas están hechas de cerámica o madera, con un centro hueco y orificios con áreas iguales o desiguales que son cubiertas para producir diferentes notas; esta dificultad se puede remediar usando un material dócil. Este material tiene que ser de forma alargada, cilindrica y de consistencia maciza para evitar una deformación posterior; además, tal material debe permitir labrar el instrumento cómodamente. Entre las posibles opcio­nes disponibles se eligió a una zanahoria (aunque parezca inusual) pues reúne todos los requisitos para la construcción de la ocarina; el único inconveniente es su sensibilidad al paso del tiempo ya que su volumen se puede reducir por la deshidratación.

Descriptores: instrumentos musicales — propiedades acústicas de sólidos

ABSTRACT

In pre Colonial wind instruments sound is produced through the vibration of an air column such as in the Quena, Zampona and Tarka. A less well known wind instrument of the same family is the Ocarina whose fabrication and tuning are particularly difficult. The Ocarina is a small wind instrument with a high pitch (523 - 1046 kHz) and is found in many forms and designs. The instrument is arduous to make given that it is usually crafted from materials such as ceramic or wood and is composed of a hollow centre and finger holes of varying or equal diameter This difficulty can be remedied by using a more pliable and yet durable material that can be formed into an elongated, and cylindrical form. Looking into the possible available alternative materials the carrot was chosen. The carrot met all the requirements although the material shrinks over time due to dehydration.

Subject headings: musical instruments — acoustical properties of solids

---

1.  INTRODUCCIÓN

La ocarina se remonta a la América prehispánica, a cul­turas como la aymara y la quechua que utilizaban este instrumento musical acompañados de quenas, zamponas y otros instrumentos. Se usa en países como Perú, Bolivia, Venezuela, norte de Chile, norte de Argentina y toda Me-soamérica.

Cabe recalcar que aunque existe teoría que se refiere al origen de este instrumento en Europa, se trata de otro ins­trumento de similares características ya que la Ocarina Sud-Americana tiene orígenes de cientos de años atrás.

La podemos encontrar en modelos sencillos, dobles o tri­ples y con diferente número de orificios, como muestra la Fig. 1. Su tono depende de la relación entre el volumen del aire y el área del agujero destapado. Por ejemplo, en una oca­rina de cuatro agujeros de áreas iguales, cubriendo todos los

FIG. 1.— Los tipos de ocarinas dependen del tamaño y del agujeros que posee.

 

FIG. 2.-temático.

Ocarina artesanal hecha de arcilla usada para el modelado maorificios previamente para luego pasar a quitar el dedo de uno de ellos, se obtiene la nota Sol, independientemente de qué agujero se destape. Si el área descubierta es igual, la nota producida es la misma.

2.  ESCALA PENTATÓNICA

En nuestro sistema musical occidental, es conveniente uti­lizar sólo unas frecuencias concretas, a las cuales se las llama notas.

Las frecuencias de las notas se dividen en porciones lla­madas "octavas", y cada octava se divide en 12 porciones llamadas notas. Cada nota de una octava tiene exactamente la mitad de frecuencia que la misma nota en la octava supe­rior.

Con el oído humano solamente se pueden captar notas que sean superiores a 18/fz y por debajo de los 20kHz (muy aproximadamente). Es así que sólo podemos oír unas diez octavas como mucho, con doce notas cada una. Por debajo de 18/fz se llaman infrasonidos y por encima, ultrasonidos. El margen auditivo de las personas varía según la edad y otros factores. Los animales tienen un margen auditivo diferente; así, es muy conocido el hecho que los perros pueden sentir frecuencias mucho más altas, dentro del margen de los ultra­sonidos.

Para que nuestra ocarina produzca sonidos agradables al oído humano es necesario ajustaría a una escala musical pentatónica porque es la escala más simple e intuitiva. La pentafonía —sistema musical en que se usa la escala pen­tatónica— se usa en la generalidad de los sistemas musicales tradicionales por ser usados por los músicos antiguos.

Nuestro oído humano tiene una "construcción" tal, que los sonidos cuyas frecuencias están en la proporción simple (2/1, 3/2, 4/3, etc.), suenan juntos de una manera agrada­ble. Por ejemplo, la nota Do en su quinta octava tiene apro­ximadamente una frecuencia de 1046.5Hz y junto a un Sol en la misma octava de frecuencia 1567.9 Hz suena agradable porque están a una proporción de 3:2, respectivamente. Esta proporción es la combinación de sonidos más pura y se la suele llamar quinta justa.

En un sistema musical pentafónico se necesita una nota base que es la nota más grave que puede producir nuestro instrumento y una configuración de frecuencias de las notas;

FIG. 3.— Relación lineal que existe entre el área descubierta y la frecuen­cia.

esta configuración es:

Tono, 9/8 Tono, (3/2)(8/9) = 4/3 Tono, 3/2 Tono, (3/2) (9/8) = 27/16 Tono, (3/2)²(8/9) = 2 Tono

La ocarina propuesta consta de una escala pentatónica, de cinco notas, con una nota base en Do sostenido (Do#). Y obedeciendo las reglas de esta escala su sistema musical tiene que ser como indica la Tabla 1.

 

3.  MODELO MATEMÁTICO PARA EL NÚMERO DE ORIFICIOS DE LA OCARINA

Los orificios de la ocarina son la parte más importante en el diseño de la ocarina ya que aportan la variedad tonal pro­puesta en la Tabla 1.

Así que tuvimos que diseñar un modelo que pueda relacio­nar el área del orifico con la frecuencia que deseamos obte­ner, recordando que la nota depende de la suma de orificios destapados.

Primeramente se tomó una ocarina artesanal (Fig. 2) hecha de arcilla que constaba de seis orificios de \mm de diámetro cada uno y se aumentó nueve orificios más; teniendo un total de quince orificios. La posición de los orificios fue relevante porque no perturbó en gran magnitud a las frecuencias obte­nidas.

Luego se procedió a tomar la frecuencia del total de ori­ficios descubiertos con ayuda del software Analysis Center 2010. Su diseño nos da la facilidad de poder obtener la fre­cuencia con el micrófono en tiempo real.

Las frecuencias que se obtuvieron en relación con el área destapada (Tabla 2) nos dan una idea de que existe una re­lación lineal. Esta relación se puede observar en la Fig. 3.

TABLA 2

 

 

FlG. 4.— Pasos realizados para la construcción de la ocarina. Las primeras dos fotos muestran la parte resonadora y la boquilla. Las dos últimas fotos muestran la parte que permite el flujo del aire.

Así que procedemos hacer el ajuste de curvas (1): Usando la regresión lineal observamos que>> es el área y x es la frecuen­cia. Con todo esto podemos concluir que nuestro modelo está hecho y es:

donde A es el área del orificio y i⁷ es la frecuencia deseada. O, en función del diámetro D del orificio, la cual emplea­remos más adelante para la construcción de la ocarina de za­nahoria:

4.  CONSTRUCCIÓN DE LA OCARINA DE ZANAHORIA

En la construcción se necesitaron dos zanahorias lo más uniformes posible y de mayor volumen para poder evitar po­sibles fisuras al afollar. Y los pasos fueron los siguientes:

•    Tomamos la primera zanahoria y la cortamos por la parte delgada, después con un taladro ahuecamos la za­nahoria por la porción central. Esta sirve para la parte resonante de la ocarina (Fig. 4a).

•    Hacemos un pequeño orificio cuadrangular en forma descendente en la parte central de su superficie con ayuda de un cincel y un estilete pequeño (Fig. 4b).

•    Agarramos la segunda zanahoria y la cortamos de tal

TABLA 3

manera que pueda ingresar en la primera zanahoria (Fig. 4c).

• Cortamos en la parte que se inserta en la primera za­nahoria un canal cuadrangular que permite el flujo de aire (Fig. 4d).

Cuando pasamos al último paso, el tallado de los orificios, tenemos que hacer uso del modelo (2) y la Tabla 1.

Reemplazamos la frecuencia de la segunda nota (porque la primera la obtenemos sin necesidad de orificios) en (2) y obtenemos el diámetro del primer orificio, es decir, con F = 775.2 se obtiene D = 6.7mm.

Para el segundo orificio debemos modificar (2) porque si lo usáramos directamente obtendríamos el área necesaria más el área del primer orificio obteniendo datos que no nos sirven de manera inmediata. Es por ello que usaremos:

 

Donde F es la frecuencia requerida y F₀ es la frecuencia de la nota previa. Con este proceso obtenemos los diámetros re­queridos para las frecuencias de las notas deseadas (Tabla 3). Se puede deducir que esta escala tiene una tendencia a ori­ficio de 6mm. Lamentablemente estas medidas no se pue­den conseguir a cabalidad porque se necesitaría algún instru­mento que pueda perforar con una exactitud de micrómetros

5.  PRUEBA DE SONIDO Y ANÁLISIS ESPECTRAL

Ya construida la ocarina ahora pasamos a analizar su afi­nación, es decir, con un análisis espectral observamos los pi­cos más altos de frecuencia frente a su amplitud. Estos picos obtenidos gracias a las herramientas del software MATLAB 7.4.0 como la transformada rápida de Fourier (FFT) nos di­cen su acercamiento a la nota musical que esperamos obte­ner.

Inicialmente de manera un tanto obvia podemos asegurar que las notas más graves, de manera específica las tres pri­meras notas (Fa, Sol y La# ) suenan mejor afinadas que las ultimas tres (Do, Re y Fa), posiblemente por la variación en la octava a que corresponden. Pero más específicamente se puede ver por las gráficas obtenidas que se muestran en la Figs. 5 a 10, que las dos primeras notas tienen una mayor precisión respecto al tono.

La frecuencia de la primera nota Fa de la cuarta octava (nuestra nota base) tuvo un rango de frecuencia entre 660 Hz y 680 Hz, se acercó bastante al resultado esperado, exacta­mente unos 9AHz de diferencia (Fig. 5).

En la segunda nota Sol (Fig. 6) se esperó que diera 115.2Hz y obtuvimos un rango entre 160Hz y 780Hz. El re­sultado requerido se encuentra dentro de nuestro rango. Sin embargo, se observa que el rango va en aumento.

.

FlG. 9.— Esta gráfica corresponde a la frecuencia de la quinta nota Re.

Los resultados de las notas La sostenido y Do tienen una similitud bastante interesante: Para la nota La sostenido cal­culamos una frecuencia de 918.8/fz, y en la Fig. 7 vemos

FlG. 10.— Esta gráfica corresponde a la frecuencia de la sexta nota Fa.

que la mayor amplitud se encuentra entre 900Hz y 950Hz; en la cuarta nota Do se calculó una frecuencia de 1033.6Hzy como se muestra en la Fig. 8 se observa una mayor amplitud entre 1000Hz y 1050Hz. Las Figs. 7 y 8 muestran un inter­valo de mayor amplitud, de 50Hz y la frecuencia calculada está dentro de los rangos.

Cuando las notas de nuestra ocarina subieron a una quinta octava el sonido de las notas Re y Fa simplemente ya no se escuchó y esto se puede ver en la gran dispersión de las Figs. 9 y 10.

6.  CONCLUSIONES

La ocarina, y en especial esta ocarina hecha de un vege­tal muy común, tiene una cierta ventaja en la construcción pero una seria desventaja de duración puesto que mientras el tiempo se prolongue su sonido irá decayendo en claridad ya que la boquilla se deshidrata cada vez más perdiendo el corte en el flujo que hace el sonido. Otro problema con este instrumento es que, como explicamos en su construcción, la zanahoria que dirige el flujo del aire tiene que caber exac­tamente sin dejar que escape el aire del resonador, y por el mismo problema de la deshidratación este va perdiendo vo-lumeny cada vez deja escapar más aire, cambiando las notas y el tono del instrumento.

Pero al estar éste fresco, ésto es, aproximadamente unos dos días después de la inmediata construcción, puede darnos sonidos muy claros, variados y afinados de la manera que se requiera. Si usamos notas que pertenezcan a la cuarta o ter­cera octava obtendremos sonidos mucho más claros porque el instrumento hecho de zanahoria no alcanza frecuencias tan altas demandadas para la quinta octava en adelante.

Y se puede decir que este es el instrumento más senci­llo, de bajo costo y sorprendente, porque al no depender de la resonancia, es decir, siendo su forma relevante a la hora de la construcción, se puede formar de materiales orgánicos—aunque parezca humorístico— como pepinos manzanas o hasta muy difícilmente de huevo, porque estos tienen un gran volumen y una gran versatilidad al momento de su cons­trucción.

REFERENCIAS

1.-  Halliday, R. & Krane. 1998, Física, vol. 1, cuarta ed. (CECSA)        [ Links ]^rND^sHalliday^nR.^rND^nA. R.^sTicona Bustillos^rND^nG. M.^sRamírez Ávila^rND^nA. R.^sTicona Bustillos^rND^nG. M.^sRamírez Ávila^rND^nA. R^sTicona Bustillos^rND^nG. M^sRamírez Ávila

CONDICIONES DE SINCRONIZACIÓN EN DOS PÉNDULOS ACOPLADOS

Sinchronization Conditions of Two Coupled Pendula

A. R. Ticona Bustillos¹, G. M. Ramírez Ávila^1,2

¹Instituto de Investigaciones Físicas, Universidad Mayor de San Andrés
Casilla 8635, La Paz, Bolivia
²AG Nichtlineare Dynamik (S) / Kardiovasculäre Physik
Institut für Physik
Humboldt-Universität zu Berlin, Robert-Koch-Platz 4, 10115 Berlin, Alemania
(Recibido 5 de febrero de 2010; aceptado 7 de marzo de 2010)

---

Abstract

Based on a damped pendulum discrete model, we studied the synchronization conditions for two coupled pendula, varying both the pendula's features and coupling conditions. We found the basis for attraction in several situations in which the control parameters were fixed. Varying the control parameters (length, mass and damping coefficient), we found phase diagrams related to the initial conditions of one of the pendula; in these diagrams we identified synchronization regions. We emphasize the synchronization with a winding number ρ ≈ 1 (synchronization 1:1); nevertheless, other synchronization orders are possible (ρ ≠ 1).

Subject headings: dynamical systems (non-linear) - synchronization - coupled oscillators Código(s) PACS: 05.45._a, 05.45.Xt

Resumen

Con base en un modelo discreto de péndulo amortiguado, se estudian las condiciones de sincronización para dos péndulos acoplados, variando las características propias de los péndulos, así como las condiciones de acoplamiento. Se encuentran las cuencas de atracción para diferentes situaciones en las que se fijan los parámetros de control. Variando los valores de los parámetros de control (longitud, masa y coeficiente de disipación), se encuentran diagramas de fase relacionados con las condiciones iniciales de uno de los péndulos, mediante los cuales es posible identificar regiones de sincronización. Se hace énfasis en la sincronización 1:1 aunque sincronizaciones de otros órdenes son también posibles.

Descriptores: sistemas dinámicos no-lineales - sincronización - osciladores acoplados

---

1  Introducción

El fenómeno de sincronización es muy común en la naturaleza y muchos sistemas de diversa índole exhiben este comportamiento [212003Strogatz,172003Rosenblum & Pikovsky], destacándose entre ellos los sistemas biológicos [42001Glass], las reacciones químicas [192003Shabunin et al.Shabunin, Astakhov, Demidov, Provata, Baras, Nicolis, & Anishchenko,32005Fukuda et al.Fukuda, Morimura, & Kai], los circuitos electrónicos [91998Kittel et al.Kittel, Parisi, & Pyragas,132003 Ramírez Ávila et al. Ramírez Ávila , Guisset, & Deneubourg], los láseres [181994Roy & Thornburg,112009López-Gutiérrez et al.López-Gutiérrez, Posadas-Castillo, López-Mancilla, & Cruz-Hernández] y por supuesto, los péndulos [71986Huygens,202003Smith et al.Smith, Blackburn, & Baker] que desde el punto de vista histórico, constituye el primer sistema en el cual se observó sincronización [61673Huygens]; los péndulos, a pesar de ser sistemas en apariencia simples siguen concitando la atención y son sujetos de investigación tanto desde el punto de vista teórico como experimental [22009Baker & Blackburn]. En este trabajo, nos abocamos a encontrar las condiciones de sincronización para dos péndulos acoplados. Se sabe que para sistemas no lineales disipativos, es posible la existencia de más de un atractor, por lo que diferentes condiciones iniciales pueden evolucionar hacia cualquiera de los atractores coexistentes; así, el conjunto de condiciones iniciales que se aproxima a un atractor, es llamado la cuenca de atracción de este atractor [81999Kapitaniak & Bishop]. En §2 se describe el modelo utilizado para estudiar el sistema de dos péndulos acoplados con disipación, en la primera parte de §3 se muestran diferentes cuencas de atracción del sistema que nos dan una idea de cómo obtener condiciones de sincronización; posteriormente, se muestran las regiones de sincronización, que pueden asociarse a las llamadas lenguas de Arnold (en el sentido de que representan regiones de sincronización de una manera similar a la utilizada en [162001Pikovsky et al.Pikovsky, Rosenblum, & Kurths,122004 Ramírez Ávila ]¹) para diferentes situaciones en las que los parámetros varían. Se darán finalmente en §4 las conclusiones y las perspectivas de este trabajo.

2  Modelo

Al igual que en [142008 Ticona Bustillos & Ramírez Ávila ], utilizamos el modelo discretizado de péndulo y lo adaptamos para la situación en la cual se tienen dos péndulos acoplados con disipación, cuyas ecuaciones están dadas por:

l θt + 1(1) = θt(1) + b(1) ( θt(1) − θt − 1(1) − K(1) sinθt(1) ) + w m(1) sinθt(2) θt + 1(2) = θt(2) + b(2) ( θt(2) − θt − 1(2) − K(2) sinθt(2) ) + w m(2) sinθt(1) , (1)

donde los superíndices 1 y 2 identifican a cada uno de los péndulos acoplados² y w representa las condiciones de acoplamiento, la cual contiene a la distancia de separación entre los péndulos y a la rigidez del material usado para acoplar los mismos; además:

b(i) = 1 1 + λ(i) m(i) ∆t    y    K(i) = g∆t2 l(i) ,

(2)

con i = 1, 2.

Figure 1: Cuenca de atracción para identificar las regiones de sincronización 1:1 (regiones oscuras) cuando la relación de longitud de los péndulos acoplados es l₂ = 2l₁ con ρ = 1.0000 ± 0.0020. Se observa una simetría en la región de sincronización que nos lleva a interpretar que la sincronización 1:1 es favorecida cuando las condiciones iniciales son bastante diferentes.

Figure 2: Cuenca de atracción delimitando las situaciones en las que ρ = 1.0000 ± 0.0001 (región oscura), cuando se considera que las masas de las lentejas de los péndulos son de 0.050 kg y 1.000 kg respectivamente. La sincronización 1:1 es favorecida cuando las condiciones iniciales de ambos péndulos tienen valores similares y con el mismo signo (extremos inferior izquierdo y superior derecho), tienen valores similares con diferente signo (región casi rectilínea con pendiente aproximada de -1) o tienen valores diferentes pero con el mismo signo y con la particularidad que uno de los péndulos debe tener una condición inicial no muy lejana a cero (el resto de las regiones de sincronización).

Este modelo fue comparado con valores experimentales en [142008 Ticona Bustillos & Ramírez Ávila ], dando muy buenos resultados, con lo que pudimos estudiar las principales características de transmisión de movimiento en función de las características del sistema. Además, se pudo verificar la fuerte dependencia de este sistema con las condiciones iniciales y algunas características de sincronización, las cuales estudiamos con más detalle a continuación.

3  Resultados

Primeramente, se determinaron las cuencas de atracción para posibles situaciones en las cuales se pueden controlar ciertos parámetros, como la masa de la lenteja y la longitud del péndulo, la disipación y el factor de acoplamiento. Para el trabajo numérico, se utilizó el valor de la aceleración debida a la gravedad en La Paz: g = 9.775 m/s²; este valor ya fue utilizado en [142008 Ticona Bustillos & Ramírez Ávila ], para comparar los resultados con medidas experimentales, las cuales fueron realizadas en esta ciudad. Analizamos el comportamiento de la relación ρ = T₂/T₁ = 1 de los períodos de los péndulos, variando las condiciones iniciales de los mismos. Esta consideración, nos permite identificar las condiciones iniciales para las cuales es posible la sincronización 1:1 entre los péndulos. Tomamos condiciones iniciales desde -0.7 hasta 0.7 rad. Nuestro primer estudio (Figs. 1-2) implica el establecimiento de las regiones de sincronización 1:1 (regiones oscuras) de las que no siguen esta relación (regiones claras), utilizando los siguientes valores para el factor resultante de disipación y el factor de acoplamiento: b⁽¹⁾ = b⁽²⁾ = 0.9999 y w = 1×10⁻⁶ respectivamente. Cada punto mostrado en estas figuras corresponde a un promedio de ρ obtenido sobre las 50 últimas oscilaciones consideradas en las simulaciones para cada péndulo. En la Fig. 1 mostramos un caso en el cual ambos péndulos tienen una masa de 0.0500 kg y los largos son de 1.00 m y 2.00 m, respectivamente. Los puntos nos muestran los valores obtenidos para ρ a partir de las diferentes condiciones iniciales, donde hacemos la distinción entre las regiones en las cuales se presenta la sincronización 1:1 (oscura) de las que no presentan esta característica (clara). Podemos observar que la región en forma de cruz corresponde a las condiciones de sincronización 1:1 ya que se obtienen valores de ρ muy cercanos a la unidad. Es interesante observar la simetría en la Fig. 1, lo que nos indica por una parte que el conjunto de condiciones iniciales que nos llevan a ρ ≈ 1 es bastante reducido y por otra parte que para obtener esta situación, las condiciones iniciales de ambos péndulos deben ser muy próximas a cero o en su defecto, uno de los péndulos debe tener una condición inicial cercana a cero y el otro un ángulo inicial considerable, situación que da lugar a que la región de sincronización 1:1 se ensanche. Esto último implica que es más fácil alcanzar una sincronización 1:1 entre los péndulos cuando uno de ello empieza en el reposo relativo (θ₀ = 0) y el otro con una amplitud grande.

Figure 3: Cuenca de atracción cuando l₁ = l₂ = 1.00 m y m₁ = m₂ = 0.050 kg, fijando b⁽¹⁾ = b⁽²⁾ = 0.999 con ρ = 1.0000 ± 0.0004 en las regiones de sincronización, las cuales presentan cierta simetría en el sentido que los péndulos deben tener condiciones iniciales de signo contrario cuando los ángulos iniciales son pequeños. Es notable también el ensanchamiento de las regiones de sincronización a medida que se consideran condiciones iniciales mayores. Se observa finalmente la aparición de una nueva región de sincronización no simétrica para valores pequeños del ángulo inicial del péndulo 2.

Figure 4: Cuenca de atracción para longitudes y masas iguales para los péndulos, con b⁽¹⁾ = b⁽²⁾ = 0.9999, cuando se considera un factor de acoplamiento w = 5×10⁻⁶. Las regiones de sincronización oscuras corresponden al valor ρ = 1.0000 ± 0.0021. Existe una simetría entre estas regiones y se nota que la densidad de las mismas es mayor que en los anteriores casos.

Para los resultados de la Fig. 2 el largo de ambos péndulos es de 1.00 m y las masas son de 0.050 kg y 1.000 kg respectivamente. En este caso, se observa que también existe una simetría en las regiones de sincronización 1:1, donde se pueden resaltar tres aspectos interesantes, a saber: (i) Los extremos inferior izquierdo y superior derecho presentan una simetría que implica que las condiciones iniciales de ambos péndulos deben tener valores similares y del mismo signo. (ii) La región rectilínea de pendiente negativa muestra que los péndulos deben comenzar cada uno en extremos opuestos para favorecer la sincronización 1:1. (iii) Las otras regiones de sincronización muestran que los valores de las condiciones iniciales pueden ser bastante diferentes pero deben tener el mismo signo y además uno de los péndulos debe comenzar con un ángulo pequeño no muy alejado de cero. En las Figs. 3 y 4 utilizamos valores iguales para los largos y las masas de ambos péndulos (l₁ = l₂ y m₁ = m₂), fijando el valor de b⁽¹⁾ = b⁽²⁾ = 0.999. En la Fig. 3, la densidad de regiones de sincronización 1:1 es mayor, resaltando las regiones en las cuales los ángulos iniciales deben ser pequeños para ambos péndulos y de diferente signo (parte central), notándose luego un ensanchamiento considerable a medida que los ángulos iniciales son mayores; se observa también la aparición de nuevas regiones de sincronización no simétricas como la que aparece en la parte central y derecha de la Fig. 3, en la cual, ambos ángulos iniciales tienen valores positivos pero el del péndulo 2 puede permanecer cercano a cero, en tanto que el del péndulo 1 puede crecer linealmente. Finalmente, en la Fig. 4 fijamos el factor de acoplamiento en w = 5×10⁻⁶. La distribución de las regiones de sincronización es parecida a la de la Fig. 3 pero estas regiones se ensanchan, lo que nos lleva a pensar que gracias al mayor acoplamiento entre los péndulos, la sincronización 1:1 se ve favorecida. Nuevamente, la lógica de condiciones iniciales de la misma magnitud pero de signos contrarios son las que llevan a la sincronización 1:1; sin embargo, como se señaló anteriormente, existe un aumento notorio de estas regiones con una tendencia a ocupar gran parte del plano θ₀₂ vs. θ₀₁. También se pueden observar manchas difusas representando regiones de sincronización 1:1 lo que muestra una vez más la tendencia que tienen las regiones de sincronización a hacerse más extensas, máxime si el factor de acoplamiento aumenta su valor. A continuación, se estudian la sincronización cuando se hacen variar un parámetro de control y las condiciones iniciales del segundo péndulo, fijando los valores del primer péndulo en: m₁ = 0.050 kg y l₁ = 1.00 m, siendo la condición inicial del primer péndulo en todos los casos θ₀₁ = 0.5 rad. De esta manera, se obtienen las regiones que guardan similitud con las lenguas de Arnold como se mencionó anteriormente, por lo que se utilizará en lo sucesivo esta terminología.

Figure 5: (Color online) Plano de fases l₂ vs. θ₀₂ para el cual se muestra la lengua de Arnold correspondiente a ρ = 1.0000 ± 0.0289 (región oscura identificada con 1), cuando m₁ = m₂ = 0.050 kg. Las otras regiones que se identifican con 0, 2-7 corresponden a zonas en las que se pueden encontrar otros órdenes de sincronización con ρ = (0,1), ρ = (1,2), ... , ρ = (6,7). Es claro que en estos intervalos, ρ ⊂ P⁺ por lo que no sólo existen regiones de sincronización sino también cuasi-periodicidades y caos.

Figure 6: (Color online) Plano de fases l₂ vs. θ₀₂ para el cual se muestra la lengua de Arnold correspondiente a ρ = 1.0000 ± 0.0201 (región oscura identificada con 1), cuando m₁ = 5m₂ = 0.050 kg. Las regiones identificadas con los números 0, 2, 3, 4 y 5 corresponden a regiones en las cuales ρ = (0,1), ρ = (1,2), ρ = (2,3), ρ = (3,4) y ρ = (4,5) respectivamente. Se nota el desplazamiento del eje de simetría hacia la izquierda (θ₀₂ < 0), lo que repercute en el hecho que la región 5 sólo se presente en la parte derecha del plano. Las regiones blancas en forma de "dedos" al interior de la lengua de Arnold es posible que sean el resultado de los errores del cálculo numérico pues si se considera un intervalo ligeramente mayor para el valor de ρ de la lengua de Arnold, estas desaparecen.

Figure 7: Plano de fases m₂ vs. θ₀₂ para el cual se muestra la lengua de Arnold correspondiente a. ρ = 1.0000 ± 0.0005 (región oscura identificada con 1), cuando l₁ = l₂ = 1.00 m. Se evidencia la presencia de regiones para ρ = (0,1) y ρ = (1,2), (regiones identificadas con 0 y 2) aunque muchas de las regiones, sobre todo las identificadas con 0, en realidad pueden ser consideradas como parte de la lengua de Arnold ρ ≈ 1 puesto que la precisión numérica es mayor a la que se puede obtener experimentalmente.

En primer lugar tomamos en cuenta la variación del largo del segundo péndulo, consideramos valores desde 0.10 m hasta 50.00 m, la masa de la lenteja de este péndulo es mantenida en 0.050 kg. En las Figs. 5-11, se muestran las regiones equivalentes a las lenguas de Arnold, donde nos concentramos en la región con ρ ≈ 1, aunque, otras regiones con otros órdenes de sincronización pueden estar también presentes. En la Fig. 5, se muestra el diagrama de fase l₂ vs. θ₀₂, en el cual aparece claramente la lengua de Arnold con ρ ≈ 1 (región oscura identificada con el número 1). Además, se identifican regiones en las que ρ toma valores comprendidos en los intervalos (0,1), (1,2), ... , (6,7) que se identifican con los números 0, 2, ... . , 7 respectivamente. Es interesante notar que estas regiones, en general, están bien definidas y son simétricas respecto de la situación en la cual θ₀₂ = 0. Modificando el valor del coeficiente de disipación, no se notan cambios apreciables, pero cambiando el valor de la masa del segundo péndulo, por ejemplo a 0.010 kg, constatamos que la lengua de Arnold para ρ ≈ 1 es más extensa que en el caso de masas iguales de las lentejas de ambos péndulos, como se puede observar en la Fig. 6. Además, se constata que la simetría existente en el caso anterior (Fig. 5) se rompe y se podría pensar que el eje de simetría ya no pasa por θ₀₂ = 0, sino que está desplazado a la izquierda del plano (θ₀₂ < 0). Como en el anterior caso, se identifican otras regiones en las cuales ρ = (0,1), ρ = (1,2), ... , ρ = (4,5), identificando las mismas con los números 0, 2, ... , 5 respectivamente, siendo ρ real y positivo lo que puede dar lugar a regiones en las cuales el comportamiento de los péndulos es periódico, cuasi-periódico o caótico. Un aspecto interesante es la aparición de regiones claras al interior de la lengua de Arnold; en principio, esto significaría que regiones con ρ < 1 rompen la simetría de la lengua de Arnold: Sin embargo, estas regiones en particular si bien poseen ρ < 1, este valor es muy cercano a 1 por lo que se podría pensar que los errores propios del cálculo numérico hacen que no se consideren estas regiones en el intervalo elegido para ρ. Otro aspecto a resaltar es la aparición de una pequeña región ρ = (4,5) sólo en la parte derecha del plano; esto se justifica fácilmente por el hecho de la ruptura de simetría referida líneas arriba. Ahora, fijando l₁ = l₂ = 1.00 m y variando el valor de m₂, podemos observar en la Fig. 7 que la lengua de Arnold para ρ ≈ 1 ya no tiene una estructura sencilla como era el caso en las Figs. 5-6 y ocupa varias regiones del plano, el cual contiene también regiones con ρ = (0,1) y ρ = (1,2). Nuevamente, nuestros resultados son conservadores en cuanto a la región de sincronización 1:1 puesto que la precisión numérica que se considera supera la precisión que se podría tener en las mediciones experimentales, por lo que es posible que las regiones de sincronización 1:1 ocupen una extensión mayor en el plano de fases m₂ vs. θ₀₂. Por otra parte, es interesante notar que en la zona en la cual m₂ ≈ m₁, se tiene una tendencia a que la región de sincronización esté presente casi para todos los valores de θ₀₂, lo que en cierta manera confirma los resultados obtenidos en la Fig. 3.

Figure 8: Plano de fases m₂ vs. θ₀₂ para el cual se muestra la lengua de Arnold correspondiente a. ρ = 1.0000 ± 0.0006 (región oscura identificada con 1), cuando l₂ = 2l₁ = 2.00 m. También existen regiones en las cuales, ρ = (0,1) y ρ = (1,2), (regiones identificadas con 0 y 2), pero al igual que en los anteriores casos, ρ = (0,1) puede ser absorbida por la región de sincronización 1:1.

En cambio si l₂ = 2l₁ = 2.00 m, la lengua de Arnold en el plano m₂ vs. θ₀₂ es muy pequeña, como se ve en la Fig. 8. Es claro que la mayor parte del plano corresponde a valores ρ = (1,2) por lo que en estas regiones bien podrían haber sincronizaciones de otros órdenes, cuasi-periodicidades o caos. Se observa también que cuando m₂ → m₁, las únicas condiciones iniciales θ₀₂ que preservan la sincronización 1:1 son aquellas en las que θ₀₂ → 0, en concordancia con los resultados de la Fig. 1. Los anteriores resultados indican que tanto la masa de la lenteja como la longitud del péndulo juegan papeles importantes en la sincronización de los dos péndulos acoplados. De igual manera podemos analizar la sincronización en función del factor de acoplamiento. En la Fig. 9 se nota que para valores pequeños del factor de acoplamiento, existe sincronización casi para todas las condiciones iniciales, en cambio para valores grandes de dicho factor, la sincronización parece desaparecer dando lugar a una "granularidad" en la que se tienen valores de ρ = (0,2). En la Fig. 9, se consideraron masas de las lentejas de los péndulos iguales pero no las longitudes de los mismos; sin embargo, el comportamiento cuando se tiene l₁ = l₂ no se modifica sustancialmente. Finalmente, si variamos el valor del coeficiente de disipación λ = λ⁽¹⁾ = λ⁽²⁾ tenemos que para péndulos con las mismas características (l₁ = l₂ y m₁ = m₂), la región de sincronización 1:1, abarca casi todo el plano de fases, como se puede observar en la Fig. 10. Regiones con ρ = (0,1) y ρ = (1,2) están también presentes en el plano pero al igual que en los anteriores casos, las regiones con ρ = (0,1), en general pueden ser absorbidas por las regiones de sincronización 1:1, lo que aumentaría aún más la densidad de regiones con ρ ≈ 1. Otro aspecto interesante es el referido a los valores elevados de λ, para los cuales, la sincronización se pierde; esto está en relación con el hecho de que cuando la disipación es muy grande, los péndulos tienden a volver a su situación de reposo relativo y las medidas de comportamiento síncrono de los péndulos ya no es posible hacerlas con un transientes adecuado.

Figure 9: Plano de fases w vs. θ₀₂ para el cual se muestra la lengua de Arnold correspondiente a. ρ = 1.0000 ± 0.0248 (región oscura identificada con 1), cuando l₂ = 2l₁ = 2.00 m y m₁ = m₂ = 0.050 kg. La región de sincronización 1:1 está bien definida para valores w ≈ 5x10⁻⁶; para valores mayores, ya no se encuentra una región bien definida para la sincronización 1:1 y se tiene una especie de "granularidad" con valores para ρ comprendidos en el intervalo (0,2).

En cambio si las longitudes de los péndulos son diferentes, la región de sincronización 1:1 se reduce drásticamente, como se puede observar en la Fig. 11. Trabajando con ρ = 1.0000 ± 0.0013 se observa que la lengua cerca de la parte central contiene regiones blancas y grises que en principio significan valores de ρ = (0,1) y ρ = (1,2) respectivamente; sin embargo, si se considera ρ = 1.0000 ± 0.0097, estas regiones desaparecen de la lengua, la cual queda bien definida y además, la región correspondiente a valores elevados del coeficiente de disipación considerados en el plano, pasa a ser considerada como región de sincronización 1:1. En este último caso, se puede pensar también que el hecho de trabajar con valores elevados del factor de disipación λ, no permite cuantificar adecuadamente las oscilaciones tal como se explicó para la Fig. 10. El hecho que la región de sincronización 1:1 sea relativamente pequeña concuerda con los anteriores resultados para situaciones en las que l₁ ≠ l₂ (Figs. 1 y 8), en las cuales se tiene la misma situación; sin embargo, no se debe olvidar los resultados mostrados en las Figs. 5 y 6 en las cuales, el intervalo de condiciones iniciales θ₀₂ que conducen a la sincronización 1:1 crece con la longitud l₂.

4  Conclusiones y Perspectivas

Se determinaron las cuencas de atracción para varios valores de parámetros, pudiéndose observar que las mismas presentan diferentes formas según el valor que toman los parámetros. Nos concentramos en las condiciones iniciales de los péndulos para las que puede existir sincronización 1:1.

Figure 10: Plano de fases λ vs. θ₀₂ para el cual se muestra la lengua de Arnold correspondiente a. ρ = 1.0000 ± 0.0006 (región oscura identificada con 1), cuando l₂ = l₁ = 1.00 m y m₁ = m₂ = 0.050 kg. Otras regiones con ρ = (0,1) y ρ = (1,2) aparecen pero es notable la predominancia de la región de sincronización 1:1. En la parte superior del plano (valores elevados de λ, existe una región en la que ρ ≈ (0.96,1)

Figure 11: Plano de fases λ vs. θ₀₂ para el cual se muestra la lengua de Arnold correspondiente a. ρ = 1.0000 ± 0.0013 (región oscura identificada con 1), cuando las longitudes de los péndulos son diferentes: l₂ = 2l₁ = 2.00 m y m₁ = m₂ = 0.050 kg. Las regiones blancas y grises que aparecen sobre la lengua, así como la región blanca en la parte superior, son regiones con ρ ≈ 1 pero con menor precisión de la establecida al principio; por lo que se espera que sean parte de la lengua con sincronización 1:1.

Se han identificado las regiones de sincronización para varias condiciones de los péndulos, en función a las condiciones iniciales del péndulo 2. Si bien nos abocamos a la determinación de la sincronización de orden 1:1, es claro que existen otros órdenes de sincronización. Además, como se tienen valores de ρ  ⊂ P⁺, pueden existir también comportamientos cuasi periódicos y caóticos. Se puede observar que la longitud y la masa de los péndulos ejercen una gran influencia en la sincronización. Se ve claramente en todos los casos estudiados, la importancia de la precisión numérica con la que se trabaja y su relación con la exactitud que se puede lograr en mediciones experimentales. A partir de estos resultados, podemos analizar cuasi periodicidades, diagramas de bifurcación, rutas hacia el caos, en las regiones donde no existe sincronización. Evidentemente, este modelo es susceptible a ampliarse a más de dos péndulos lo que constituye la continuación natural de esta investigación. Una parte importante de nuestra investigación es trabajar tanto con mediciones experimentales como con modelos que justamente son validados por estas mediciones. Si bien, por el momento se tienen concordancias importantes entre los resultados experimentales con los obtenidos a partir del modelo, no se descarta para el futuro considerar el sistema de ecuaciones diferenciales para describir el sistema de péndulos acoplados. Finalmente, se pretende que este tipo de trabajos pueda a posteriori encontrar su aplicación también en aspectos académicos y didácticos, tal como ocurrió con la primera parte de nuestra investigación con péndulos [152010 Ticona Bustillos & Ramírez Ávila ].

Agradecimientos

Agradecemos los valiosos comentarios de los árbitros de la revista, gracias a los cuales pudimos expresar con mayor claridad las ideas de este trabajo. GMRA agradece al Deutscher Akademischer Austausch Dienst (DAAD) por la beca de investigación otorgada.

 

References

[12002Bai et al.Bai, Lonngren, & Sprott]

1.- Bai, E.-W., Lonngren, K. E., & Sprott, J. C. 2002, Chaos, Solitons & Fractals, 13, 1515         [ Links ]

[22009Baker & Blackburn]

2.- Baker, J. L. & Blackburn, J. L. 2009, The Pendulum: A Case Study in Physics (Oxford: Oxford University Press)         [ Links ]

[32005Fukuda et al.Fukuda, Morimura, & Kai]

3.- Fukuda, H., Morimura, H., & Kai, S. 2005, Physica D: Nonlinear Phenomena, 205, 80         [ Links ]

[42001Glass]

4.- Glass, L. 2001, Nature, 410, 277         [ Links ]

[52003Grosu]

5.- Grosu, I. 2003, Master-slave synchronization and control of chaotic Sprott circuit (11th International IEEE Workshop on Nonlinear Dynamics of Electronic Systems, Scuol/Schuls, Switzerland)         [ Links ]

[61673Huygens]

6.- Huygens, C. 1673, Horologium Oscillatorium (Paris: Apud F. Muguet)         [ Links ]

[71986Huygens]

7.- -. 1986, The pendulum clock or geometrical demonstrations concerning the motion of pendula as applied to clocks (Iowa: Ames, Iowa : Iowa State University Press)         [ Links ]

[81999Kapitaniak & Bishop]

8.- Kapitaniak, T. & Bishop, S. R. 1999, The Illustrated Dictionary of Nonlinear Dynamics and Chaos Chichester (John Wiley & Sons, Inc.)         [ Links ]

[91998Kittel et al.Kittel, Parisi, & Pyragas]

9.- Kittel, A., Parisi, J., & Pyragas, K. 1998, Physica D: Nonlinear Phenomena, 112, 459         [ Links ]

[102004Li et al.Li, Chen, Cai, & Zhao]

10.- Li, Y.-N., Chen, L., Cai, Z.-S., & Zhao, X.-Z. 2004, Chaos, Solitons & Fractals, 22, 767         [ Links ]

[112009López-Gutiérrez et al.López-Gutiérrez, Posadas-Castillo, López-Mancilla, & Cruz-Hernández]

11.- López-Gutiérrez, R. M., Posadas-Castillo, C., López-Mancilla, D., & Cruz-Hernández, C. 2009, Chaos, Solitons & Fractals, 42, 277         [ Links ]

[122004 Ramírez Ávila ]

12.- Ramírez Ávila, G. M. 2004, Synchronization phenomena in light-controlled oscillators (PhD thesis)         [ Links ]

[132003 Ramírez Ávila et al. Ramírez Ávila , Guisset, & Deneubourg]

13.- Ramírez Ávila, G. M., Guisset, J. L., & Deneubourg, J. L. 2003, Physica D: Nonlinear Phenomena, 182, 254         [ Links ]

[142008 Ticona Bustillos & Ramírez Ávila ]

14.- Ticona Bustillos, A. R. & Ramírez Ávila, G. M. 2008, Revista Boliviana de Física, 14, 121         [ Links ]

[152010 Ticona Bustillos & Ramírez Ávila ]

15.- -. 2010, Revista Boliviana de Física, 16, 41         [ Links ]

[162001Pikovsky et al.Pikovsky, Rosenblum, & Kurths]

16.- Pikovsky, A., Rosenblum, M., & Kurths, J. 2001, Synchronization: a universal concept in nonlinear sciences, vol 12 (New York: Cambridge University Press)         [ Links ]

[172003Rosenblum & Pikovsky]

17.- Rosenblum, M. & Pikovsky, A. 2003, Contemporary Physics, 44, 401         [ Links ]

[181994Roy & Thornburg]

18.- Roy, R. & Thornburg, K. S. J. 1994, Physical Review Letters, 72, 2009         [ Links ]

[192003Shabunin et al.Shabunin, Astakhov, Demidov, Provata, Baras, Nicolis, & Anishchenko]

19.- Shabunin, A., Astakhov, V., Demidov, V., Provata, A., Baras, F., Nicolis, G., & Anishchenko, V. 2003, Chaos, Solitons & Fractals, 15, 395         [ Links ]

[202003Smith et al.Smith, Blackburn, & Baker]

20.- Smith, H. J. T., Blackburn, J. A., & Baker, G. L. 2003, International Journal of Bifurcation and Chaos, 13, 7         [ Links ]

[212003Strogatz]

21.- Strogatz, S. H. 2003, Sync: The Emerging Science of Spontaneous Order (New York: Hyperion Press)         [ Links ]

[221994Sugawara et al.Sugawara, Tachikawa, Tsukamoto, & Shimizu]

22.- Sugawara, T., Tachikawa, M., Tsukamoto, T., & Shimizu, T. 1994, Physical Review Letters, 72, 3502        [ Links ]

Footnotes:

¹Estas regiones de sincronización se diferencian de las lenguas de Arnold, en el sentido que en lugar de representarlas en un plano intensidad de acoplamiento vs. frecuencia, son representaciones en el plano parámetro de control vs. condiciones iniciales. ²Por razones de comodidad en la notación, se utilizará a lo largo del artículo m_i = m⁽ⁱ⁾ y l_i = l⁽ⁱ⁾.

---

File translated from T_EX by T_TH, version 3.89.
On 8 Nov 2010, 09:37.