ARTÍCULO

 

Innovative optimization of iron ore blending in daily mine planning from a linear programming model

 

Optimización innovadora de la mezcla de mineral de hierro en la planificación minera diaria desde un modelo de programación lineal

 

 

Vidal Félix Navarro Torresª, Edilaila Moraes^b
aVale Institute of Technology, Belo Horizonte, Minas Gerais, Brazil, vidal.torres@itv.org
^b Vale S.A, Belo Horizonte, Minas Gerais, Brazil, edilaila.moraes@vale.com
Artículo recibido: 16.10.2019 Aceptado en: 04.11.2019

 

 

---

Abstract:

This work aims to develop models and algorithms to mine planning to explore opportunities for better use of mineable reserves, seeking to optimize economic and quality objectives, in an integrated way. The research methodology aims to understand the mine planning processes and tools applied, and to identify requirements that guide the development of mathematical models to support the decisions to reuse opportunity materials (i.e. materials before considered as waste can be reevaluated due to changes in mining plans, processing technologies more evolved, increase in commodity prices, etc.)  and minimizing the variability of ROM grades in short-term planning. Analysis of operational configurations that support greater flexibility in the handling and storage of opportunity materials were also held in order to enable an objective comparison between the economic benefits of the approach and the costs and investments involved.

Keywords: daily, mine planning, optimization, linear programming.

---

Resumen:

Este trabajo tiene como objetivo desarrollar modelos y algoritmos para la planificación minera y explorar oportunidades para un mejor uso de las reservas explotables, buscando optimizar los objetivos económicos y de calidad, de manera integrada. La metodología de investigación tiene como objetivo comprender los procesos y herramientas de planificación minera aplicados, e identificar los requisitos que guían el desarrollo de modelos matemáticos para respaldar las decisiones de reutilizar materiales de oportunidad (es decir, los materiales que antes se consideraban desechos pueden ser reevaluados debido a cambios en los planes de minería, tecnologías de procesamiento más evolucionadas, aumento de los precios de los productos básicos, etc.) y minimización de la variabilidad de los grados ROM en la planificación a corto plazo. También se realizó un análisis de las configuraciones operativas que respaldan una mayor flexibilidad en el manejo y almacenamiento de los materiales de oportunidad para permitir una comparación objetiva entre los beneficios económicos del enfoque y los costos e inversiones involucrados.

Palabras clave: planificación minera, optimización, programación lineal. 

---

 

 

1.        Introduction

The definition of the ultimate pit of an ore reserve is associated with different economic and technical parameters that directly affect the viability of the company. The orebody is represented by a block model, and each block of this model is associated with an economic value that can represent a gain (if the block is classified as ore) or a cost (if the block is classified as waste). The objective of mine planning is to generate a mining sequence that optimizes economic and quality objectives, seeking the best possible use of the deposit and respecting the restrictions imposed by the production process. At the interface between the mine and the processing plant, aspects such as quality of ore and its availability in the pits are crucial to the accomplishment of production targets. The objective of mine planning and scheduling is to perform an optimization of the selection of the blocks to be mined, in order to attend the blending constrains imposed by the plant.

However, a common difficulty to all economic optimization algorithms for final pits regards to the fact that the ultimate pit limits cannot be determined until the economic values of the blocks are known with greater accuracy [2]. Actually, the economic values of the blocks cannot be known precisely until the mining sequence is specified. Hence, the mining schedule cannot be specified until the final limits are well defined, according to Carmo [3, 8]. Such recurrences suggest an iterative process that requires careful att ention of those responsible for mine planning. Still, according to Rubio [4], the process of determining the mine production plan should be done after the definition of the economic step, scheduling and the cut-off grades, which leads to simplification of the optimization problem. The algorithms assign a default value to blocks without incorporating blending concepts or extraction strategy; there is no integration of operational variability and reserves characteristics in the calculation of production schedules.

The problem of recovery of mineral deposits is closely linked to methods for calculating the cut-off grade and therefore, the ultimate pit design [1]. The benefit function of each block allows determining the ultimate pit economically feasible, which depends on several variables, in particular the cut-off grade, which depends on commodity prices and technologies involved, directly influencing the life of the mine, the average grade of the reserve and the company actual value. The global average grade of an exploitable reserve is an important parameter because it expresses, with some variability, the material that can be turned into product.

The cut-off grade is a response to the non-homogeneous nature of the materials exposed in working faces. Higher and lower grades materials can be blended, resulting in better use of the reserve and in a more homogeneous feed to the plant. However, while the cut-off grade definition for one variable leads to a correct routine, the application of various cut-off grades, in order to control the quality of more variables, may lead to under-utilization of reserves. Due to the rising trend of reduction in quality of mineral reserves, is crucial to control the several variables [5].

The parameterization of reserves is a widely used method for obtaining mass parameters and average cut-off grades. The simple parameterization seeks determining a grade-tonnage curve for the reserve, setting different cut-off grades to obtain the expected average grade. The parameters for various cuts, in turn, establishes cut-off grades for the variables of interest, but seeks to minimize the deviation obtained by performing different cutting grades. Finally, the multivariable parameterization does not consider pre-established cut-off grades and seeks to determine a curve for obtaining a desired average grade.

Multivariate parameterization methods have been studied more carefully, given the potential for better utilization of the existing ore in reserve, despite the increased implementation complexity [6]. Alternatively, mathematical integer programming techniques allow the development of optimization models for optimal selection of the ore body blocks that, when properly blended, meet the specifications of physical and chemical quality of the process. Maximizing the reservation involves selecting the larger amount of quality blocks, respecting the precedence relations and the pit slope. Mathematical models that address this problem typically deal with instances of great complexity, requiring the development of specific technical solution [7].

 

2.         Objectives

The objective of this work is the development and evaluation of mathematical models that support the decision-making process of mine production planning aiming to better use of mineable reserves and seeking lower variability of the feed grades of the processing plant in the short term planning, from optimizing the blending from planning and daily scheduling of mining.

To achieve this main objective will be determined optimal ways for the use of mineable reserves, through the evaluation of the blending of ore and waste blocks for a given planning horizon; short-term production programs will be improved, in order to minimize the variability of quality parameters in the power of processing plants; and different operational scenarios and their impact on the viability and performance of the proposed plans will be evaluated.

 

3.      Methods

3.1. Mathematical modelling

The short-term planning seeks to determine a subset of blocks to be exploited in order to meet mass and quality targets during a given period, monthly, quarterly, semiannual or yearly. However, when attention turns to the daily operations, it is essential that the feeding of processing plants have the minimal variation around the average quality. This is important to avoid negative impacts on the operating parameters and the key factors of plant performance. Thus, for daily schedule for monthly production, the exploitation order of the blocks must be such that the average quality of the total mass fed to the plant have the smallest possible variation over time. In this way, it was developed a preliminary model and two different approaches: the lower daily variation around the monthly average and lower daily variation.

The proposed model seeks to maximize the ROM mass supplied in a plan, by selecting ore blocks presented in a set that represents the planning horizon, according to the following objective function:

                                              (1)

Subject to the following constraints:

                                           (2)

                                           (3)

Where:

k: 1, 2, ... K: periods (for daily schedule, K = 30);

mi: block mass i ∈ B;

tij: grade of j ∈ (Q+ ∪ Q− ) present in the block i ∈ B;

lj : limit of j ∈ (Q+ ∪ Q− ) in the total mass;

yik: selection of block i ∈ B in the period k, yik ∈ {0, 1}.

This objective function seeks to maximize the total selected mass from the available blocks in the plan.

The lower daily variation around the monthly average approach uses the following objective function:

                        (4)

Where wj is the relative importance of the parameter j ∈ (Q+ ∪ Q−) compared with the other, as wj ∈ [0, 1] and Pj wj  = 1

Subject to the following constraints:

                                       (5)

                                                       (6)

                                       (7)

The objective function aims to minimize the sum of the daily quality deviations related to the monthly average, for each parameter. The constrains require that each block only could be used once in the considered plan, and guarantee that the daily feed capacity of the processing plant have not be exceeded.

The next formulation do not allow that large variation occur from one day to another, this formulation seeks to minimize the average daily variation, in order to minimize impacts on the processing plant. The lower daily variation approach use the following objective function:

                (8)

                (9)

                                        (10)

Subject to the following constraints:

                                          (11)

                                                     (12)

                                        (13)

                                                      (14)

                                                    (15)

                                                        (16)

3.2. Application development

Two different tools were developed.

a)      Maximize the overall mass of ore from the set of blocks available in the planning horizon. The weighted average of the quality of selected blocks must meet the quality specifications of the power plant.

b)      Minimize the daily variability of feeding the processing plants, by determining the optimal sequence of exploitation of certain blocks in the mining plan.

 

For both approaches described above, the final product comprises an integrated set of technologies to facilitate the use. The models were implemented using Python programming language, in connection with the solver Gurobi through the API available for that language. The models were integrated into an Excel spreadsheet through SolverStudio supplement. This is the spreadsheet user interface, and use is where the parameters and input data is defined for the problem.

Figure 1 Application integrated interface running to solve the optimization model

3.3. Application on real cases

The application of this work has its focus in open pit iron mines. In general, iron ore can be divided into two main types: hematite (high iron grade ore, with more than 63% grade) and itabirites (rocks formed by alternating quartz and hematite beds).

The application of the proposed model provides a higher theoretical baseline to the quality levels reached in that reserve, considering the blending of one or more blocks. For monthly plans, the selected blocks are positioned so that there is need to consider schedule and precedence constrains. In addition, the manipulation of materials geographically and temporally distant in the pit may require a feasibility analysis of the construction and use of intermediate stockpiles, which can be more consistently evaluated through simulation models of discrete events.

 

4.      Results and discussion

For an evaluation of the solution provided by the updated model, two fundamental aspects of the solutions provided by the model are illustrated. First, we highlight the daily variation in the quality parameters around the monthly average, which is the objective function of the model. Figure 1 to Figure 4 show graphs of this variation to the databases of the two mines provided: Mine 1 and Mine 2.

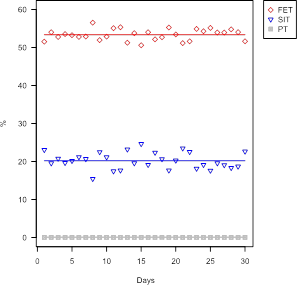
Figure 1 Daily variation of contents, for Mine 1

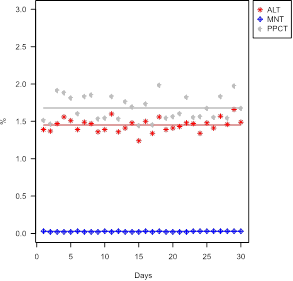
Figure 2 Daily variation of contents, for Mine 1

Figure 3 Daily variation of contents, for Mine 2

 

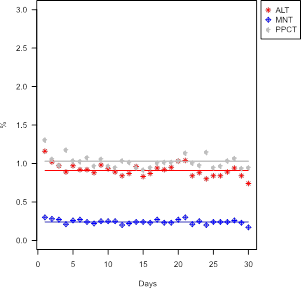
Figure 4 Daily variation of contents, for Mine 2

 

Finally, it was indicated the monthly mass value of ore achieved, compared with the possible upper limit of the processing plant. Figure 5 and Figure 6 illustrates the total weight for each of the quality parameters for both Mine 1 and 2.

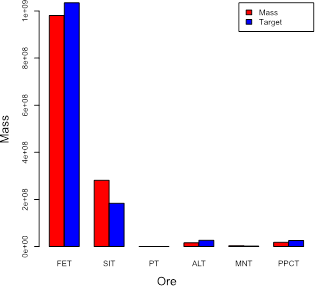
Figure 5 Total monthly mass in the sequence determined by the model for the Mine 1

 

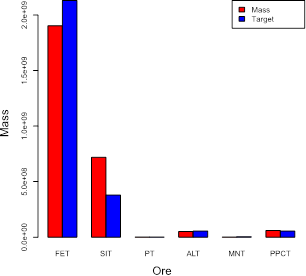
Figure 6 Total monthly mass in the sequence determined by the model for the Mine 2

 

4.      Conclusions

Through testing it was found that the implementation of the model, its extent and the corrections made satisfy the demand, and the results of optimization were fully satisfactory in the context of the daily mine planning.

The implementation of the model, using the Gurobi solver, allows executing the instance chosen by the user and optimizing the planning of daily sequencing exploitation of mining blocks. Through an Excel spreadsheet integrated into Solver Studio is provided to the user an interface for insertion of quality targets parameters, daily mine capacity and other problem input data. Through tests, it was found that the implementation of the model, its extension and corrections made are consistent with the demand and, therefore, it is concluded that the project was successfully completed.

 

Acknowledgments

Special thanks to the work of researchers of Vale Institute of Technology (ITV) and Vale S.A. Company.

 

References

 

[1] A. S. Oliveira, L. Esawa, J. Gonçalves e T. Bianchi, “Projeto Parametrização Multivariável,” 2012.        [ Links ]

[2] A. Lamghari, R. Dimitrakopoulos e J. A. Ferland, “A variable neighbourhood descent algorithm for the open-pit mine production scheduling problem with metal uncertainty,” Journal of the Operational Research Society, vol. 65, pp. 1305-1314, 2014.        [ Links ]

[3] F. A. R. do Carmo, A. Curi e W. T. de Sousa, “Otimização econômica de explotações a céu aberto,” Revista Escola de Minas, vol. 59, n. 3, 2006.        [ Links ]

[4] E. Rubio, “Planificación Minera: Desafíos y Nuevas Tendencias en la Industria Minera,” em Primer Taller de Planificación Minera, Santiago, Chile, 2009.        [ Links ]

[5] A. C. Girodo e J. L. Beraldo, “Elementos Básicos de um Projeto de Mineração,” em Curso Projetos de Mineração, Belo Horizonte, Instituto Brasileiro de Mineração, 1981.        [ Links ]

[6] A. C. Campos, J. Valente e A. C. Girodo, “Parametrização Multivariável de Recursos e Reservas,” Brasil Mining Site, n. http://brasilminingsite.com.br/includes/modulos/mdl_artigo/exibir_artigo.php?id=24, 2008.        [ Links ]

[7] J. Amaya, D. Espinoza, M. Goycoolea, E. Moreno, T. Prevost e E. Rubio, “A scalable approach to optimal block scheduling,” em Application of Computers and Operations Research in the Mineral Industry (APCOM), Vancouver, 2009.        [ Links ]

[8] F. A. R. do Carmo, “Metodologias para o Planejamento de Cavas Finais de Minas a Céu Aberto Otimizadas,” Ouro Preto, 2001.        [ Links ]